Motion in 2 and 3 dimensions
Let us review the definitions of velocity and acceleration with the help of
two problems.
Problem:
Suppose that the position vector function for a particle is given by
r(t)
= x(t)i + y(t)j
with x(t) = at + b and y(t) = ct2 + d, where a = 1 m/s, b = 1 m, c =
0.125 m/s2, and d = 1 m.
(a) Calculate the average velocity during the time interval t = 2 s to t = 4 s.
(b) Determine the velocity and speed at t = 2 s.
Solution:
- Reasoning:
The definition of the instantaneous velocity is v = ∆r/∆t.
The definition of the instantaneous velocity is v = lim∆t-->0∆r/∆t = dr/dt.
- Details of the calculation:
(a) The position of the particle is given to us as a function of time. At t =
2 s the position of the particle is
r(2 s) = [(1 m/s)(2 s) + 1 m]i + [(0.125 m/s2)(4 s2)
+ 1 m]j = 3 m i + 1.5 m j.
At t = 4 s its position is
r(4 s) = [(1 m/s)(4 s) + 1 m]i + [(0.125 m/s2)(16 s2)
+ 1 m]j = 5 m i + 3 m j.
The average velocity of the particle between 2 and 4 seconds is
v = ∆r/∆t = (r(4 s) -
r(2 s))/(2 s),
v = [(5 m - 3 m)i + (3 m - 1.5 m)j]/(2 s) = (1 m/s)i
+ (0.75 m/s)j.
(b) The instantaneous velocity of the particle is
v = dr/dt = [d(x(t)/dt]i + [dy(t)/dt]j = ai +
2ctj.
Review derivatives if you
don't understand this.
At t = 2 s the instantaneous velocity is v(2s) = (1 m/s)i + (0.5
m/s)j.
The speed at 2 seconds is v = (vx2 + vy2)½
= (1 + 0.25)½ m/s = 1.12 m/s.
Problem:
The coordinates of an object moving in the xy-plane vary with time according
to the equations
x = (-5 m) sin(t) and y = (4 m) - (5 m) cos(t), where t is in seconds.
(a) Determine the components of velocity and components of acceleration at t =
0.
(b) Write expressions for the position vector, the velocity vector, and the
acceleration vector at any time t > 0.
(c) Describe the path of the object in an xy-plot.
Solution:
- Reasoning:
We use v = dr/dt, a = dv/dt.
- Details of the calculation:
(a) The x- and y-components of the position vector of the object are given
as a function of time.
We have vx = dx/dt = (-5 m/s) cos(t), vy = dy/dt = (5 m/s)
sin(t).
At t = 0 we have v = (-5 m/s)i.
Differentiating the velocity vector with respect to time we find
ax = dvx/dt = (5 m/s2) sin(t), ay =
dvy/dt = (5 m/s2) cos(t).
At t = 0 we have a = (5 m/s2)j.
(b) v = (-5 m/s) cos(t)i + (5 m/s) sin(t)j,
a = (5
m/s2) sin(t)i + (5 m/s2) cos(t)j.
(c) A spreadsheet can be used to construct the table below.
| t (s) |
x(t) (m) |
y(t) (m) |
|
0 |
0 |
-1 |
|
0.1 |
-0.49917 |
-0.97502 |
|
0.2 |
-0.99335 |
-0.90033 |
|
0.3 |
-1.4776 |
-0.77668 |
|
0.4 |
-1.94709 |
-0.6053 |
|
0.5 |
-2.39713 |
-0.38791 |
|
0.6 |
-2.82321 |
-0.12668 |
|
0.7 |
-3.22109 |
0.175789 |
|
0.8 |
-3.58678 |
0.516466 |
|
0.9 |
-3.91663 |
0.89195 |
|
1 |
-4.20735 |
1.298488 |
|
1.1 |
-4.45604 |
1.732019 |
|
... |
... |
... |
We can now use the spreadsheet to make a Graph [chart type XY (Scatter)
in Microsoft Excel] of the path of the object, by plotting y(t) as a
function of x(t). The path is a circle. The center of this circle lies on
the y-axis at x = 0, y = 4 m.
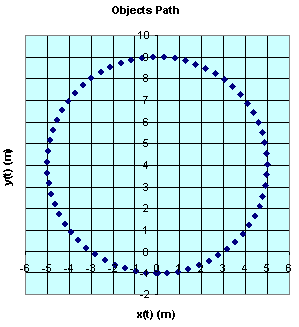
At t = 0 the particle is at x = 0, y = -1m. Its velocity vector is
pointing into the negative x-direction. The particle is moving clockwise in
a circle.
Let us now consider three-dimensional motion
with constant acceleration.
Let a = axi + ayj + azk
= (ax, ay, az) = constant. Since
a is
constant, the components ax, ay, and az are
constant and the average acceleration is equal to the instantaneous
acceleration.
Assume that at t = 0 a particle is at position r0 = x0i
+ y0j + z0k and has velocity
v0
= v0xi + v0yj + v0zk. At
time t, i.e. after a time interval ∆t = t, its velocity has changed by an amount
∆v = a∆t = at. We can rewrite this in terms of the
components as
∆vxi + ∆vyj + ∆vzk
= axt i + ayt j + azt k.
A vector equation like this is equivalent to a set of three equations, one for
each component of the vector in three dimensions.
∆vx
= ax∆t, ∆vy = ay∆t, ∆vz =
az∆t.
The x-component of the acceleration only changes the x-component of the
velocity, the y-component of the acceleration only changes the y-component of
the velocity, etc.
The velocity as a function of time is given by
vx = v0x + ∆vx
= v0x + ax∆t,
vy = v0y
+ ay∆t,
vz
= v0z∆t + az∆t,
or
v =
v0
+ a∆t.
Note: If the directions of v0 and
a are different, the direction of v is different from the direction
of v0.
For constant acceleration the motions along the perpendicular axes
of a Cartesian coordinate system are independent and can be
analyzed separately.
The position of the particle at time t is given by
x = x0 + v0x∆t + ½ax∆t2,
y = y0
+ v0y∆t + ½ay∆t2,
z = z0
+ v0z∆t + ½az∆t2,
or
r = r0 +
v0∆t + ½a∆t2.
Note: The directions of r0,
v0,
a, and r may all be different. If
a is constant then the x, y, and z-coordinated as a function
of time can be found independently.
Problem:
At t = 0, a particle moving in the xy-plane with constant acceleration has a
velocity v0 = (3i - 2j) m/s at the origin. At t
= 3 s, the particle's velocity is v = (9i + 7j) m/s. Find
(a) the acceleration of the particle and
(b) the coordinates at any time.
Solution:
- Reasoning:
For motion with constant acceleration we have
v =
v0
+ a∆t,
r = r0 +
v0∆t + ½a∆t2.
- Details of the calculation:
(a) We are told that the particle moves with constant acceleration and we are
given its velocity vector at t = 0 and t = 3 s.
a = ∆v/∆t = (v(3 s) -
v0)/(3 s) = (9 m/s
- 3 m/s)i/(3 s) + (7 m/s + 2 m/s)j/(3 s).
a = (2 m/s2)i + (3 m/s2)j.
(b) At t = 0 the particle is at the origin, r0 = 0.
Therefore r = v0t + ½at2 is its
position at time t.
r = [(3 m/s)t + (1 m/s2)t2]i + [(-2 m/s)t +
(1.5 m/s2)t2]j.
x(t) = (3 m/s)t + (1 m/s2)t2, y(t) = (-2 m/s)t + (1.5 m/s2)t2.
Problem:
A particle originally located at the origin has
an acceleration of a = 3j m/s2 and an initial velocity
of v0 = 5i m/s.
(a) Find the vector position and velocity at any time t.
(b) The coordinates and speed of the particle at t = 2 s.
Solution:
- Reasoning:
For motion with constant acceleration we have
v =
v0
+ a∆t,
r = r0 +
v0∆t + ½a∆t2.
- Details of the calculation:
(a) A particle is moving with constant acceleration. At t = 0 it is at the
origin and its velocity v0 is given. Its position at any time
t is r = v0t + ½at2.
r = (5 m/s)ti + (1.5 m/s2)t2j.
The particles velocity at time t is v = v0 +
at.
v = (5 m/s)i + (3 m/s2)tj.
(b) At t = 2 s the coordinates of the particle are x = 10 m and y = 6 m.
Its speed is
v = (vx2 + vy2)½ = (25
+ 36)½ m/s = 7.81 m/s.
