Work done by a constant force

Assume you are lifting an object with mass 20 kg from the ground to a height of 1.5 m.  Assume that you are exerting a constant force in the upward direction and that you are moving the object upward with uniform velocity.  The net force on the object is zero.  The force you are exerting is equal in magnitude and opposite in direction to the force of gravity.  As you are lifting the object you are doing work on the object.

The work W done on an object by a constant force is defined as W = F·d.  It is equal to the magnitude of the force, multiplied by the distance the object moves in the direction of the force.
In the example above F = mg = (20 kg)(9.8 m/s²) = 196 N, W = (196 N)(1.5 m) = 294 Nm.

Work is a scalar, a number with units.  The SI unit of work Nm = Joule (J).

Work is the "scalar product" or "dot product" of the force and the displacement vector.  The scalar product of two vectors A and B is a scalar quantity (a number with units) equal to the product of the magnitudes of the two vectors and the cosine of the smallest angle between them.

A·B = ABcosθ.

In terms of the Cartesian components of the vectors A and B the scalar product is written as

A·B = A_xB_x + A_yB_y + A_zB_z.

The work done by a force can be positive or negative.  If the component of the force in the direction of the displacement is positive, then the work is positive, and if the component of the force in the direction of the displacement is negative, then the work is negative.  In one dimension, the scalar product is positive if the two vectors are parallel to each other, and it is negative if the two vectors are anti-parallel to each other, i.e. if they point in opposite directions.

Example:

Assume you forgot to set the parking break and your car starts rolling down a hill.  You try in vain to stop it by pulling as hard as you can on the bumper, but the car keeps on moving forward.  You exert a force on the car opposite to the direction of travel.  The distance traveled in the direction of the force is negative, you do negative work on the car.  But the car is pulling you in the direction of travel with a force of equal magnitude (Newton's third law).  The car is doing positive work on you. 

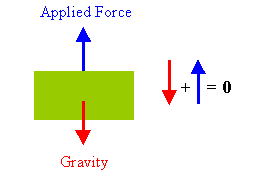A free-body diagram of an object being lifted with constant velocity through a distance d is shown on the right.
The net force on the object is zero, F_a + F_g = 0.
The displacement vector points in the upward direction. 
The work done by the applied force F_a, W = F_a·d = F_ad = mgd, is positive. 
The work done by the gravitational force F_g, W = F_g·d = -F_gd = -mgd, is negative. 
The net work done by all forces acting on the object W_net = F_net·d is zero.

Problem:

For A = 3i + j - k, B = -i + 2j + 5k, and C = 2j - 3k, find C·(A - B).

Solution:

• Reasoning:
  Evaluate the scalar product of two vectors.
• Details of the calculation:
  A = 3i + j - k.  B = -i + 2j + 5k.  A - B = 4i - j - 6k.  C = 2j - 3k.  C·(A-B) = -2 + 18 = 16.

Problem:

Explain why the work done by the force of sliding friction is negative when an object undergoes a displacement on a rough surface?

Solution:

• Reasoning:
  The force of sliding friction always points in a direction opposite to that of the velocity v = dr/dt.  It therefore points in a direction opposite to that of the displacement dr. dW = F_f·dr = -F_fdr.

Problem:

When a particle moves in a circle, a force acts on it, directed towards the center of rotation.  Why is it that this force does no work on the particle?

Solution:

• Reasoning:
  Since at any point along the circle the centripetal force is perpendicular to the velocity v and therefore to the displacement dr, the scalar product dW = F·dr is zero.

Problem:

While mowing a lawn, a boy pushes a lawn mower a total distance of 350 m over the grass with a force of 90 N directed along the horizontal.  How much work is done by the boy?

Solution:

• Reasoning:
  The work done on an object by a constant force is defined as W = F·d = Fdcosθ.
  Here F and d point in the same direction, θ = 0, cosθ = 1.
• Details of the calculation:
  W = F·d = 90 N * 350 m = 31500 J.

Problem:

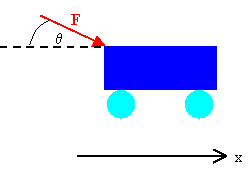A shopper in a supermarket pushes a cart with a force of 35 N directed at an angle of 25^o downward from the horizontal.  Find the work done by the shopper as he moves down an aisle of 50 m length.

Solution:

• Reasoning:
  The work done on an object by a constant force is defined as W = F·d = F_x∆x + F_y∆y + F_z∆z.
  The cart is moving in the x-direction, ∆y = ∆z = 0.
  The x-component of the force is F_x = Fcosθ = (35 N)cos(25^o).
  Only the x-component of the force does work, since there is no displacement of the cart in the y-direction.
• Details of the calculation:
  The work done by the shopper is W = F_x∆x = (35 N)cos(25^o)(50 m) = 1586 J.

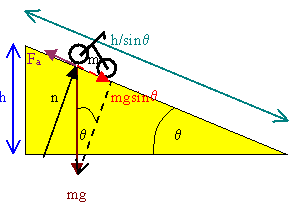Ramps

Assume you want to lift your motorcycle onto the bed of your pickup truck.  You probably will use a ramp.  You will choose a long board.  One end of the board will rest on the bed of the truck and the other end will rest on the ground.  You will roll your motorcycle up this ramp.

You apply a force F_a equal in magnitude and opposite in direction to the component of the gravitational force parallel to the ramp.  The magnitude of F_a is mgsinθ.  You move the motorcycle a distance h/sinθ in the direction of the force.  The work you do is W = F·d = mgh, where mg is the weight of your motorcycle and h is the height of the bed.  If you would lift the motorcycle straight up, you would exert a force equal to its weight through a distance h.  When rolling it up the ramp, you have to push on it through a much longer distance.  To do the same work, you therefore need a much smaller force.  The ramp provides mechanical advantage.

Work = large force × small distance = small force × large distance.

Work done by a varying force in one dimension

If you are not familiar with integrals please follow this link before gong on.

A short review of definite integrals

The work done by a varying force F with only an x-component is defined as 
W = ∫_xi^xf F(x)dx = lim_∆x-->0 Σ_xi^xf F(x)∆x.
(The symbol Σ  stand for the sum.  Σ_xi^xf F∆x is the sum of the products F∆x from the initial to the final position in steps of ∆x.) 
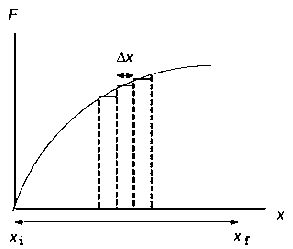
We can plot the component of the force F acting on the object at position x versus the position x.
The work done by the force is equal to the area under the curve.

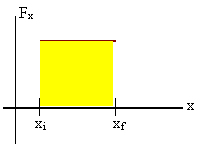A plot for a constant force acting from x_i to x_f is shown on the right.
The work done by the force is W = F(x_f - x_i).

Work done by a varying force in three dimensions

In three dimensions the work done by a varying force is W = ∫_ri^rf F·dr = lim_∆r-->0Σ_ri^rf F·∆r.
Here dr is an infinitesimally small segment of the path from the initial to the final position.  In terms of the components of F and dr the integral can be written as
∫_path F·dr = ∫_path F_xdx + ∫_path F_ydy + ∫_path F_zdz.

Lifting an object near the surface of Earth

In order to lift an object of mass m so that its height increases by a distance h, you have to exert an average force mg through a distance h. 
The work you have to do lifting the object is W = mgh.

Problem:

A 100 N crate sits on the ground and is attached to one end of a rope.  A person on a balcony pulls up on the rope with a constant force of 100 N, lifting the crate a distance of 3 m.
(a)  How much work is done by the person?
(b)  How much work is done by gravity?

Solution:

• Reasoning:
  The person pulls up and the crate moves up, in the direction of the force.
  The work done by the person is positive, W = Fd = mgd = (100 N)d.
  The 100 N force of gravity points down while the crate moves up.  Gravity does of negative work.
• Details of the calculation:
  (a)  The work done by the person is W = (100 N)*(3 m) = 300 J.
  (b)  Gravity does 300 J of negative work.

Problem:

(a)  Calculate the work done on a 1500 kg elevator car by its cable to lift it 40 m at constant speed, assuming friction force averages 100 N.
(b)  What is the work done on the elevator car by the gravitational force in this process?

Solution:

• Reasoning:
  The elevator car weighs 1500*9.8 N = 14700 N.  To make the car move at constant speed, the net force on it must be zero.  The force the cable exerts on the car must have a magnitude of 14800 N, to cancel the weight and the 100 N frictional force pointing in the opposite direction.  The cart moves in the direction of force exerted by the cable, so the work done by this force is positive.
• Details of the calculation:
  (a)  The work done by the cable is W_cable = (14800 N)*(40 m) = 5.92*10⁵ J.
  (b)  The work done on the elevator car by the gravitational force is W_g = -(14700 N)*(40 m) = -5.88*10⁵ J.
  This work is negative since the displacement points in the opposite direction of the force.