Kepler's laws
Newton's law of gravitation states that any two objects with masses m1 and m2, respectively, attract each other with a force proportional to the product of their masses and inversely proportional to the square of the distance R between them.
F = Gm1m2/R2
The proportional constant G = 6.67*10-11 Nm2/kg2 is a constant of nature. Mass m1 pulls on mass m2, and mass m2 pulls on mass m1. The center of mass of each object is pulled towards the center of mass of the other object.
Two astronomical objects, such as the sun and a planet, pull each other towards their common center of mass. Each object accelerates towards the center of mass. The acceleration of object 1 is a1 = Gm2/R2, and the acceleration of object 2 is a2 = Gm1/R2. If each object has velocity perpendicular to the direction of its acceleration and v12/R1 = a1, v22/R2 = a2, with R1 and R2 being the distances of object 1 and object 2 from the CM, then both objects orbit their common CM in circular orbits. If object 1 is much more massive than object 2, then the CM lies very close to the center of object 1. For example, the CM of the Sun-Earth system lies inside the Sun. Then R2 is approximately equal to R and we can write
Gm1/R = v22.
If object 2 is in a circular orbit about a much more massive object 1, its speed is given by this formula. All nine planets orbit the sun in approximately circular orbits. Their orbital speeds are related to their orbital radii. We may write v2 = 2πR/T2, where T2 is the period of the planet. We then have
Gm1/R = (2πR/T2)2, or T22 = (4π2/Gm1)R3.
The square of the period of a planet in a circular orbit is proportional to the cube of the orbital radius.
Not all orbits are circular. The obits of the planets are approximately, but not exactly circular. The planets' orbits are elliptical. (A circular orbit is a special case of an elliptical orbit.) When two objects orbit each other under the influence of a force that decreases as 1/R2, then their orbits will be elliptical.
Kepler's Three Laws of Planetary Motion
In the 16th century, the Polish astronomer Nicolaus Copernicus replaced the traditional Earth-centered view of planetary motion with one in which the Sun is at the center and the planets move around it in circles. Although the Copernican model came quite close to correctly predicting planetary motion, discrepancies existed. This became particularly evident in the case of the planet Mars, whose orbit was very accurately measured by the Danish astronomer Tycho Brahe. The problem was solved by the German mathematician Johannes Kepler. Kepler found that planetary orbits are not circles, but ellipses. Kepler described planetary motion according to three laws. Each of these laws is illustrated by an applet.
-
Law I: Each planet revolves around the Sun in an
elliptical path, with the Sun occupying one of the foci of the ellipse.
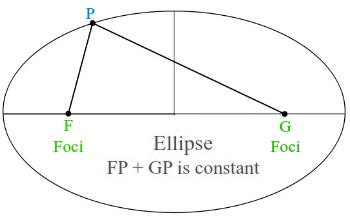
-
Law II: The straight line joining the Sun and a planet
sweeps out equal areas in equal intervals of time.
Kepler's second law is a consequence of conservation of angular momentum.
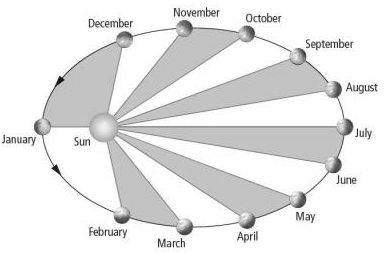
Since the direction of the gravitational force is towards the center of mass (~the sun), it does not exert a torque about the CM. The angular momentum about the CM, L = r × p is therefore constant. Since p = mv, we have L = mr × v, and r × v = constant. The area swept out by the straight line joining the Sun and a planet per unit time is equal to (1/2)r × v (it is the area of a triangle) and therefore is constant. - Law III: The squares of the planets' orbital periods are
proportional to the cubes of the semi-major axes of their orbits.
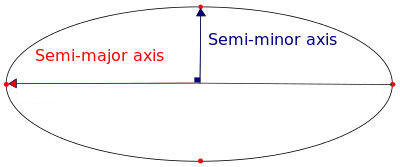
Kepler's laws apply not just to planets orbiting the Sun, but to all cases in which one celestial body orbits another under the influence of gravitation -- moons orbiting planets, artificial satellites orbiting the Earth and other solar system bodies, and stars orbiting each other.
Link:
- The Physics Classroom: Kepler's laws
Problem:
At what position in its elliptical orbit is the speed of a planet a maximum? At what position is the speed a minimum?
Solution:
- Reasoning:
Kepler's second law: r × v = constant.
The speed has its maximum value when the planet-sun distance has its minimum value. The speed has its minimum value when the planet-sun distance has its maximum value.
Problem:
Io, a satellite of Jupiter, has an orbital period of 1.77 days and an orbital radius of 4.22*105 km. From these data, determine the mass of Jupiter.
Solution:
- Reasoning:
Kepler's third law: T22 = (4π2/Gm1)R3.
Let object 1 be Jupiter, and object 2 be Io. m1 >> m2. - Details of the calculation:
m1 = (4π2/GT22)R3
= 4π2(4.22*108 m)3/((6.67*10-11 N m2/kg2)(1.77*24*60*60 s)2) = 1.9*1027 kg.
Problem:
Haley's Comet approaches the sun to within 0.570 A.U., and its orbital period is 75.6 years. (A.U. is the abbreviation for astronomical units, where 1 A.U. =1 .5*1011 m is the mean Earth-Sun distance.) How far from the sun will Haley's comet travel before it starts its return journey?
Solution:
- Reasoning:
Kepler's third law: T22 = (4π2/Gm1)R3.
Let object 1 be the sun, and object 2 be the comet. m1 >> m2.
For elliptical orbits, R denotes the semi-major axis, R = (Rmax + Rmin)/2. - Details of the calculation:
R3 = Gm1T2/4π2.
R3 = (6.67*10-11 Nm2/kg2)(1.991*1030 kg)(75.6*365*24*60*60 s)2/4π2
= 1.91*1037 m3.
R = 2.67*1012 m = (Rmax + Rmin)/2.
Rmax = 5.35*1012 m - 0.570*1.5*1011 m = 5.26*1012 m.
Rmax is the maximum distance of the comet from the sun.