What does Bernoulli's equation mean?
Bernoulli's equation
P1 + ρgh1 + ½ρv12
= P2 + ρgh2 + ½ρv22
or
P + ρgh + ½ρv2 = constant.
If a liquid is at rest, then
P1 + ρgh1
= P2 + ρgh2,
Pbottom + ρghbottom = Ptop + ρghtop,
Pbottom = Ptop + ρg(htop - hbottom).
The pressure in the fluid increases linearly with depth.
If a liquid is at rest in a horizontal pipe, P1
= P2, the pressure is the same everywhere.
A liquid flowing in a horizontal pipe
P1 + ½ρv12 = P2
+ ½ρv22.
If a liquid (or a gas which is not being compressed)
is flowing frictionless in a steady state through a horizontal
pipe with a varying cross-sectional area, then the pressure depends on the speed
of the fluid.
The faster the fluid is flowing, the lower is the pressure at the same
height.
This may seem counterintuitive to you, but it is a consequence
of conservation of energy. The molecules of a fluid at room
temperature are always in motion, even if the fluid as a whole is at rest.
This disordered motion is responsible for the pressure exerted by the fluid,
even in gravity-free space. In a pipe, it results in collisions with
the walls. If a fluid is flowing trough a horizontal pipe at a steady
rate, then the molecules also have ordered motion. In a narrow section
of the pipe the fluid is flowing faster, and more of its energy goes into
the ordered motion. This leaves less energy for the random motion and
therefore results in softer collisions and lower pressure. Phenomena which can be understood with the help of Bernoulli's equation
include the Pitot tube, the Venturi effect, atomizers, hurricanes, flapping
flags, etc.
Faster flow --> more kinetic energy in he ordered motion
--> less kinetic energy in the random motion --> lower pressure
Problem:
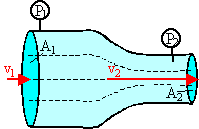 A Venturi tube may be used as a fluid flow meter. If the difference in
pressure P1 - P2 = 21 kPa, find the fluid flow rate in m3/s
given that the radius of the outlet tube is 1 cm, the radius of the inlet tube is
2 cm, and the fluid is gasoline (ρ = 700 kg/m3).
A Venturi tube may be used as a fluid flow meter. If the difference in
pressure P1 - P2 = 21 kPa, find the fluid flow rate in m3/s
given that the radius of the outlet tube is 1 cm, the radius of the inlet tube is
2 cm, and the fluid is gasoline (ρ = 700 kg/m3).
Solution:
- Reasoning:
From Bernoulli's equation we have P1 + ρgh1 + ½ρv12
= P2
+ ρgh2 + ½ρv22.
h is constant, so P1
+ ½ρv12 = P2 + ½ρv22,
or P1 - P2 = ½ρv22 - ½ρv12.
From the equation of continuity we have
Area 1*v1 = Area 2*v2. v1 = (A2/A1)v2.
- Details of the calculation:
Using P1 - P2 = ½ρv22
- ½ρv12, we have
21 kPa = 350 kg/m3
(v22 - v12).
Inserting v1
= (A2/A1)v2. into the above equation we have
(1-(A2/A1)2)v22) =
(21000/350)(m/s)2.
(A2/A1)2 = (1/4)2
= 1/16. v22
= (21000/350)(16/15)(m/s)2 = 64(m/s)2..
v2
= 8 m/s.
Volume flow rate: A2v2 =
π(0.01 m)2*8 m/s = 0.0025 m3/s.
Real fluids are not ideal fluids. But in a short enough section, the
laminar flow of a real fluid may be approximately treated as ideal, if the
energy loss in this section is very small compared to the ordered kinetic energy
of the fluid in the section. Then Bernoulli's equation is approximately
valid for this section of the real fluid.
Embedded Question 2
You roll down the window on your car while driving on the freeway. An
empty plastic bag on the floor promptly flies out the window. Explain
why.
Discuss this with your fellow students in the discussion forum!
 A Venturi tube may be used as a fluid flow meter. If the difference in
pressure P1 - P2 = 21 kPa, find the fluid flow rate in m3/s
given that the radius of the outlet tube is 1 cm, the radius of the inlet tube is
2 cm, and the fluid is gasoline (ρ = 700 kg/m3).
A Venturi tube may be used as a fluid flow meter. If the difference in
pressure P1 - P2 = 21 kPa, find the fluid flow rate in m3/s
given that the radius of the outlet tube is 1 cm, the radius of the inlet tube is
2 cm, and the fluid is gasoline (ρ = 700 kg/m3).