The human eye
External link: The Physics Classroom: Refraction and the Ray Model of Light Lesson 6 - The Eye
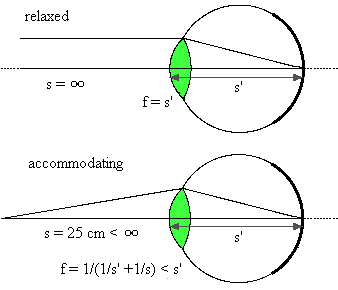 The simplest model of the human eye is a single lens with an adjustable focal
length that forms an image on the retina, or the light-sensitive bed of nerves
which lines the back of the eyeball. The eye is either relaxed (in its normal
state in which rays from infinity are focused on the retina), or it is
accommodating (adjusting the focal length by flexing the eye muscles to image
closer objects).
The simplest model of the human eye is a single lens with an adjustable focal
length that forms an image on the retina, or the light-sensitive bed of nerves
which lines the back of the eyeball. The eye is either relaxed (in its normal
state in which rays from infinity are focused on the retina), or it is
accommodating (adjusting the focal length by flexing the eye muscles to image
closer objects).
The near point of a human eye, defined to be s = 25 cm, is the shortest
object distance that a typical or "normal" eye is able to accommodate, or to image onto the
retina.
The far point of a human eye is the farthest object distance that a typical eye is able to image onto the retina. It is at infinity for the "normal" eye.
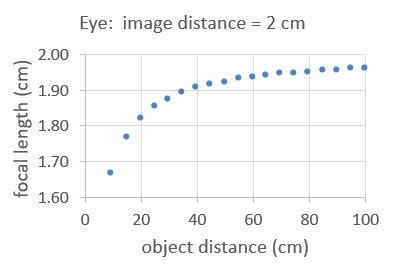
In the figure below the focal length of the accommodating normal eye is plotted versus the object distance. For the relaxed eye the focal length is 2 cm.
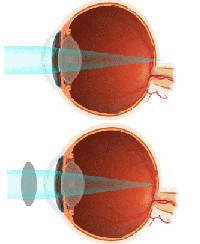
Myopia (nearsightedness)
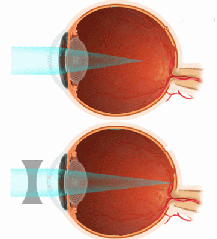 In a nearsighted eye, the cornea is too steeply curved for the length of the
eye, causing light rays from distant objects to focus in front of the retina.
Distant objects appear blurred or fuzzy because the light rays are not in focus
by the time they reach the retina. The eye is able to form images on the
retina for objects that are closer than the eye's far point, but the far point
is no longer at infinity, but is a shorter distance away from the eye.
In a nearsighted eye, the cornea is too steeply curved for the length of the
eye, causing light rays from distant objects to focus in front of the retina.
Distant objects appear blurred or fuzzy because the light rays are not in focus
by the time they reach the retina. The eye is able to form images on the
retina for objects that are closer than the eye's far point, but the far point
is no longer at infinity, but is a shorter distance away from the eye.
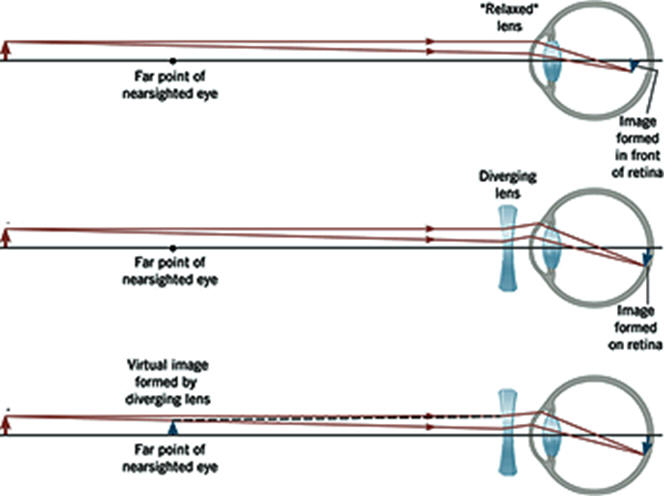
Myopia can be accommodated for through the use of a negative lens that will
cause the light rays to diverge. The power of the lens is chosen by matching the
lens' focal point with the eye's far point. The lens forms a virtual image
of very distant objects at the far point of the nearsighted eye.
Hyperopia (farsightedness)
 In contrast to myopia, hyperopia occurs when the eye is too short for the
power of its optical components. In hyperopia, the cornea is not steep
enough and light rays hit the retina before they come into focus. In the
case of hyperopia, light from distant objects is focused to a point behind the
retina by the relaxed eye. Even for distant objects some accommodation is
needed. The eye is able to form images on the retina for objects that are
farther from the eye than its near point, but the near point is no longer at 25
cm, but is a longer distance away from the eye.
In contrast to myopia, hyperopia occurs when the eye is too short for the
power of its optical components. In hyperopia, the cornea is not steep
enough and light rays hit the retina before they come into focus. In the
case of hyperopia, light from distant objects is focused to a point behind the
retina by the relaxed eye. Even for distant objects some accommodation is
needed. The eye is able to form images on the retina for objects that are
farther from the eye than its near point, but the near point is no longer at 25
cm, but is a longer distance away from the eye.
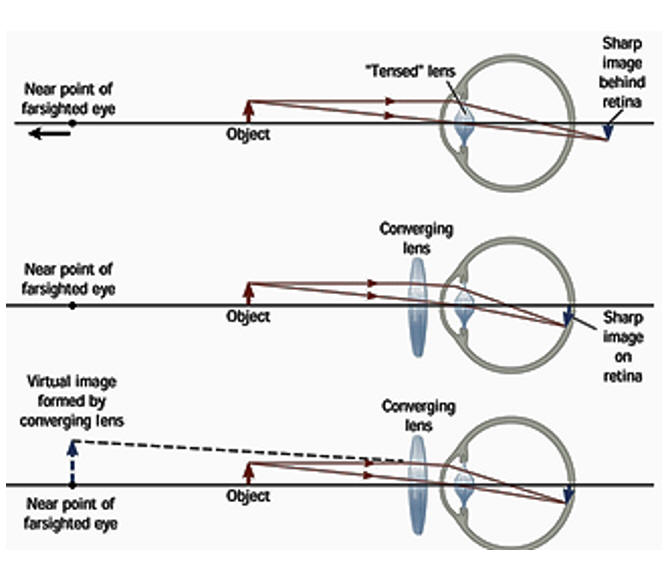
Hyperopia can be accommodated for through the use of a positive lens that will
cause the light rays to converge. The power of the lens is chosen by matching the
lens' focal point with the eye's near point. The lens forms a virtual image
of very close by objects at the near point of the farsighted eye.
Focal Length and Diopters
When making and selling eyeglasses, people prefer to speak of the lens power
P, measured in diopters D, instead of the focal length f. If you want to buy
eyeglasses, you need to know the power of the lenses. Focal length and power of
a lens are related to each other.
D = 1/f(m)
where
D = diopters, f = lens focal length (in meters), and a "+" sign indicates a
converging lens and a "-" sign indicates a diverging lens.
For
two thin lenses in contact, 1/f = 1/f1 +
1/f2, and therefore power is P = Pthin(1) + Pthin(2),
i.e. the powers of thin lenses in contact add algebraically.
Problem:
What is the power of a normal human eye in diopter when focusing on an object at the near point of the eye? Assume the lens to retina distance is 2 cm.
Solution:
- Reasoning:
The power of a lens is measured in diopters, D = 1/f(m). - Details of the calculation:
P = 1/f = 1/xo + 1/xi.
The object is at the near point, xo - 25 cm = 0.25 m. The image is on the retina, xi = 2 cm = 0.02 m.
P = 1/0.25 m + 1/0.02 m = 54/m = 54 D.
Embedded Question 3
- The cornea provides about 2/3 of the power of the eye. Light is refracted when traveling from air into the cornea. The lens provides the remaining 1/3 of the power needed to produce an image on the retina. If the lens of a person's eye is removed because of cataracts, why would you expect a eyeglasses lens of about 16 diopters to be prescribed?
- The cataract-clouded lens of the eye can be replaced an internal lens.
This intraocular lens can be chosen so that the person has perfect distant
vision.
Will the person be able to read without glasses? If the person was nearsighted, is the power of the intraocular lens greater or less than the removed lens?
Discuss your questions with your fellow students in the discussion forum!