Electric charges produce electric fields.
The electric field
produced by a point charge q at rest at the origin is
E = F/q
= (keQ/r2)
(r/r).
The electric field of a charge distribution can be found using the principle of
superposition.
Field lines can be
used to visualize the electric field.
There are no magnetic charges.
Moving electric charges produce magnetic fields.
To produce a magnetic field
B, a current
density j is needed, i.e. j = ρ+<v+> + ρ-<v->
cannot be zero.
The magnetic field produced by permanent magnets is due to "magnetization
current" densities inside ferromagnetic materials. This is
atomic-scale physics, and on that scale Classical Physics fails and
Quantum Mechanics is the model that is used. Many research
groups are currently investigating the magnetic properties of various
materials, both experimentally and theoretically, and many questions
still need to be answered.
Field lines can be used to visualize the
magnetic field.
Magnetic field lines have no beginning or end, they always form closed
loops. (Because there are no magnetic charges, there are no
sources or sinks.)
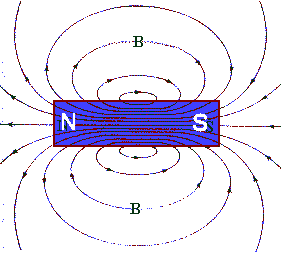 The field lines visualizing the magnetic field of a permanent bar magnet are shown on the right.
The field lines visualizing the magnetic field of a permanent bar magnet are shown on the right.
External link:
Explore the magnetic field of a bar magnet
(PhET)
We define the north and south pole of a bar magnet so
that inside the bar magnet the magnetic field points
from the south pole (S) to the north pole (N). Outside a bar magnet the field lines close the loop, from north
to south.
The density of the field lines is proportional to the strength of the magnetic
field.
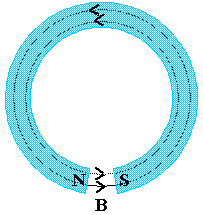 When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong.
When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong.
Currents, i.e. moving electric charges, produce magnetic fields. Maxwell's equations tell us how to compute the
electric fields and magnetic fields produced by charged particles. The terms
electrostatics and magnetostatics
refer to steady state conditions, when all charges are at rest or only steady
currents are flowing. Then the charge densities do not change anywhere.
Under those conditions Maxwell's equations are given on the below.
| (1) |
∮A E∙dA = Qinside/ε0 |
| (2) |
∮Γ E∙ds
= 0 |
| (3)
|
∮A B∙dA = 0 |
| (4)
|
∮Γ B∙ds = μ0Ithrough Γ
|
The first of these equations is Gauss' law.
It tells us that the total flux of the electric field through a closed surface is
proportional to the total charge inside the surface. In electrostatics, electric field
lines begin and end on charges. If there is no charge inside a closed surface, then there
is no source or sink of field lines inside the surface. All the field lines that enter
through the surface into the volume enclosed by the surface must also exit through the
surface. The net flux through the surface is zero.
Gauss' law
by itself can be used to find the electric field of a point charge at rest, and the
principle of superposition can then be used to find the electric field of an arbitrary
charge distribution.
The second of Maxwell's equations tells us that the
electrostatic field is a conservative field. The total work done by the
electric field on a test charge when moving it along a closed loop path is
W = q∮Γ E∙ds = 0.
Under steady state conditions, Maxwell's equations for the electric field are
decoupled from the equations for the magnetic field. The first two of Maxwell's equations
describe the properties of the electric field, while the last two describe the properties
of the magnetic field. We can calculate the electric field without considering the
magnetic field and vice versa.
The third of Maxwell's equations tells us that there are no magnetic charges, and
therefore no sources and sinks for the magnetic field. The net flux of the magnetic field
through any closed surface is zero. All the field lines that enter
through the surface into a volume enclosed by the surface also exit through
the surface. Magnetic field lines always are closed loops.
The fourth of Maxwell's equations is called Ampere's law.
It tells us that the circulation of the magnetic field
B, namely the integral of the tangential component of B along a closed curve
Γ, is proportional to the current flowing through the area
enclosed by the curve. The proportional constant μ0
= 4π10-7 N/A2 is called the
permeability
of free space.
∮Γ B∙ds = μ0Ithrough Γ
When integrating along a closed path, one must choose a
direction for ds, i.e. one must choose to move around the loop clockwise or
counterclockwise. The two directions yield the same magnitude but a different sign for the
result of the integration. The right-hand rule is again used to resolve this ambiguity.
Let your thumb point in the direction of current flow. The circulation of
B is
positive if the fingers of your right hand point in the direction of ds.
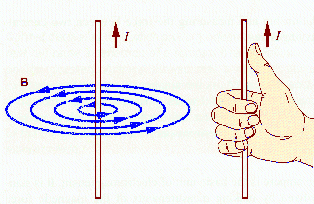 Ampere's
law can be used to find the magnetic field due to a steady current flowing in a very
long straight wire. Consider a single, isolated, long straight wire, carrying a current I.
Assume the wire is aligned with the z-axis. Symmetry considerations tell us that the
magnitude of the magnetic field produced by the current in the wire at some point P(x,y,z)
can only depend on the radial distance r = (x2 + y2)½ of P
away from the wire, not on the z-coordinate of P. If we imagine a circular loop of radius
r, then the magnetic field is tangential to the loop. The integral of the tangential
component of B along the closed curve is just the magnitude of B
times the circumference of the loop.
Ampere's
law can be used to find the magnetic field due to a steady current flowing in a very
long straight wire. Consider a single, isolated, long straight wire, carrying a current I.
Assume the wire is aligned with the z-axis. Symmetry considerations tell us that the
magnitude of the magnetic field produced by the current in the wire at some point P(x,y,z)
can only depend on the radial distance r = (x2 + y2)½ of P
away from the wire, not on the z-coordinate of P. If we imagine a circular loop of radius
r, then the magnetic field is tangential to the loop. The integral of the tangential
component of B along the closed curve is just the magnitude of B
times the circumference of the loop.
∮Γ B∙ds = B2πr = μ0Ithrough Γ.
B = μ0I/(2πr).
The proportional constant μ0 = 4π*10-7
N/A2 is called the permeability of free space.
The SI unit for the magnetic field is Ns/(Cm) = Tesla(T)
 The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude B = μ0I/(2πr).
The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current. The picture shows an iron-filing pattern, which reveals
the nature of the magnetic field surrounding a current-carrying wire.
The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude B = μ0I/(2πr).
The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current. The picture shows an iron-filing pattern, which reveals
the nature of the magnetic field surrounding a current-carrying wire.
Problem:
A 30 A current is flowing in a long, straight wire. What is the
magnetic field strength a distance 1 cm from the wire?
Solution:
- Reasoning:
The magnitude of the magnetic field field a radial distance r away from a
long, straight wire is B = μ0I/(2πr).
- Details of the calculation:
B = (4π*10-7
N/A2)*30 A/(2π*0.01 m) = 1.2*10-5/*0.02 =
N/(As) = 6*10-4 T.
For comparison,
near Knoxville, TN, the strength of the Earth magnetic field is ~ 53 microT
= 5.3*10-5 T.
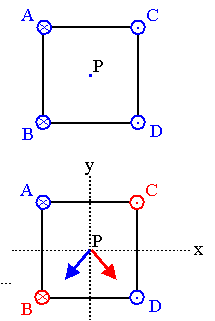 Problem:
Problem:
Four long parallel wires carry equal currents of I = 5 A. The figure
on the right is an end view of the conductors.
The current direction is into the page at points A and B and out of the
page at points C and D. Calculate the magnitude and direction of the
magnetic field at point P, located at the center of the square of edge
length 0.2 m.
Solution:
- Reasoning:
At point P, (the origin of the chosen coordinate system) wires A and
D each produce a magnetic field of magnitude μ0I/(2πd)
pointing towards wire B. Here d2 = (0.12 + 0.12)
m2. Wires C and B each produce a magnetic field of magnitude
μ0I/(2πd)
pointing towards wire D. The y-components of all the fields add, while
the x-components cancel. The total field at point P therefore has
magnitude
- Details of the calculation:
B = 4μ0I sin(45o)/(2πd)
= 80*π*10-7sin(45o)/(2π(0.2)½) T
= 20 mT and points into the negative y-direction.
Maxwell's equations can be used to derive the Biot-Savart
law. The Biot-Savart
law can be used to find the magnetic field produced by any distribution of steady
currents. For a small segment of wire of length dl carrying a current I, the
Biot-Savart law states that the magnetic field dB produced by that
segment a distance r from the segment is given by
dB(r) = km I dl ×(r-r')/|r-r'|3.
Here km is a constant, km = 10-7 Tm/A. Often km
is written as km = μ0/(4π),
where μ0 is the permeability of free space.
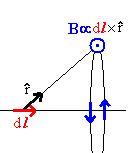 The Biot-Savart law is an inverse square law.
The Biot-Savart law is an inverse square law.
(r-r')/|r-r'|3
= 1/|r-r'|2 * (r-r')/|r-r'|
where (r-r')/|r-r'| is the unit vector pointing in
the (r-r') direction.
The directional aspects are such that the
magnetic field produced by a current element dl at any point P encircles the
straight line passing through dl.
Since steady currents always flow in closed loops, we need to integrate dB
over the entire circuit to evaluate the net field B at point P.
(This is a vector integral. The contributions dB from different sections add vectorially.) All sections of the loop contribute to
B. But because of the inverse-square dependence on distance, the sections closest to P make the largest
contributions.
B(r) = (μ0/(4π))∫circuit
I dl'×(r-r')/|r-r'|3.
Some Results
The magnetic field on the axis of a current loop
of radius R, a distance z from the center of the loop is
B = μ0IR2/(R2
+ z2)3/2 n.
Here n is a unit vector pointing in the direction of the right-hand rule, if
the fingers coil in the direction of the current flow.
At the center of the loop z = 0 and B = (μ0I/(2R))n.
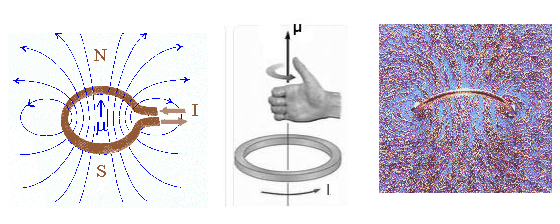 A small current loop has a magnetic dipole moment
defined as
μ = IAn. The magnetic field lines of a loop with dipole moment
μ are shown on the right. The field-line pattern
is that of a small magnet. We say that μ
points from the south pole to
the north pole of the magnet. (Magnetic field lines therefore exit a magnet at the north pole and enter at
the south pole.)
A small current loop has a magnetic dipole moment
defined as
μ = IAn. The magnetic field lines of a loop with dipole moment
μ are shown on the right. The field-line pattern
is that of a small magnet. We say that μ
points from the south pole to
the north pole of the magnet. (Magnetic field lines therefore exit a magnet at the north pole and enter at
the south pole.)
 The magnitude of
the field inside a tightly wound solenoid (away from the ends) with n = N/L
turns per unit length is
The magnitude of
the field inside a tightly wound solenoid (away from the ends) with n = N/L
turns per unit length is
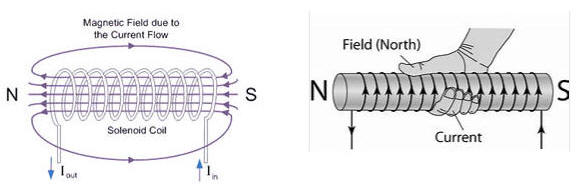
B = μ0nI.
The direction of the field is given by the right-hand rule. Curl the fingers of
your right hand in the direction that the current flows in the solenoid. Your thumb points in the direction of
B. In the picture on the right the field pattern inside a
current-carrying solenoid is revealed with iron filings.
Problem:
What current is required in the windings of a long solenoid that has
1000 turns uniformly distributed over a length of 0.4 m in order to produce
at the center of the solenoid a magnetic field of 10-4 T?
Solution:
- Reasoning:
The magnitude of
the field inside a tightly wound solenoid (away from the ends) with n = N/L
turns per unit length is B = μ0nI.
- Details of the calculation:
Near the center of the solenoid B = μ0nI
= 4π10-7(1000/0.4)*I T, with I in
units of Ampere.
With B = 10-4 T, we need I = 10-4A/(4π*10-7
2500) A
= 31.8 mA.
External link:
Explore the magnetic field produced by a coil (PhET)
Problem:
Find the
magnetic field at the center of a circular loop of radius R that is
formed in a long straight thin wire that carries current I. Use the SI
system of units.
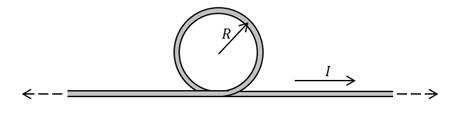
Solution:
- Reasoning:
We use the principle of superposition and add the
magnetic field of a long straight wire and a current loop.
- Details of the calculation:
Bwire(r) = μ0I/(2πR)
out of the page.
Bloop(r) = μ0I/(2R)]
out of the page.
Btotal(r) = [μ0I/(2πR)][π
+ 1] out of the page.
The right hand rule
We use a right hand rule for two different purposes.
One is to find the direction of the vector cross product. That is
covered in module 4.
The other purpose is to relate the direction of a current to the direction of
the magnetic field or to the magnetic moment it produces.
There are two cases where this works.
(a) We have current flowing in a straight wire and the magnetic field lines
form circles around the wire.
(b) We have current flowing in a wire forming a loop or a coil, and the
magnetic field in the middle of the loop or coil is perpendicular to the loop
and straight inside the coil.
In other words, we have something that is straight, and something that curls.
Then if the thumb of your right hand points in the direction of the thing that
is straight, then the fingers of you right hand curl in the same direction of
the thing that is curling, and vice versa.
 The field lines visualizing the magnetic field of a permanent bar magnet are shown on the right.
The field lines visualizing the magnetic field of a permanent bar magnet are shown on the right. When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong.
When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong. Ampere's
law can be used to find the magnetic field due to a steady current flowing in a very
long straight wire. Consider a single, isolated, long straight wire, carrying a current I.
Assume the wire is aligned with the z-axis. Symmetry considerations tell us that the
magnitude of the magnetic field produced by the current in the wire at some point P(x,y,z)
can only depend on the radial distance r = (x2 + y2)½ of P
away from the wire, not on the z-coordinate of P. If we imagine a circular loop of radius
r, then the magnetic field is tangential to the loop. The integral of the tangential
component of B along the closed curve is just the magnitude of B
times the circumference of the loop.
Ampere's
law can be used to find the magnetic field due to a steady current flowing in a very
long straight wire. Consider a single, isolated, long straight wire, carrying a current I.
Assume the wire is aligned with the z-axis. Symmetry considerations tell us that the
magnitude of the magnetic field produced by the current in the wire at some point P(x,y,z)
can only depend on the radial distance r = (x2 + y2)½ of P
away from the wire, not on the z-coordinate of P. If we imagine a circular loop of radius
r, then the magnetic field is tangential to the loop. The integral of the tangential
component of B along the closed curve is just the magnitude of B
times the circumference of the loop. The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude B = μ0I/(2πr).
The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current. The picture shows an iron-filing pattern, which reveals
the nature of the magnetic field surrounding a current-carrying wire.
The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude B = μ0I/(2πr).
The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current. The picture shows an iron-filing pattern, which reveals
the nature of the magnetic field surrounding a current-carrying wire.  Problem:
Problem: The Biot-Savart law is an inverse square law.
The Biot-Savart law is an inverse square law. A small current loop has a magnetic dipole moment
defined as
μ = IAn. The magnetic field lines of a loop with dipole moment
μ are shown on the right. The field-line pattern
is that of a small magnet. We say that μ
points from the south pole to
the north pole of the magnet. (Magnetic field lines therefore exit a magnet at the north pole and enter at
the south pole.)
A small current loop has a magnetic dipole moment
defined as
μ = IAn. The magnetic field lines of a loop with dipole moment
μ are shown on the right. The field-line pattern
is that of a small magnet. We say that μ
points from the south pole to
the north pole of the magnet. (Magnetic field lines therefore exit a magnet at the north pole and enter at
the south pole.) The magnitude of
the field inside a tightly wound solenoid (away from the ends) with n = N/L
turns per unit length is
The magnitude of
the field inside a tightly wound solenoid (away from the ends) with n = N/L
turns per unit length is
