If an object is rotating about a fixed z-axis with constant angular acceleration α, we have Δω = αΔt,

ω_f = ω_i + α(t_f - t_i).

The angular displacement θ about the z-axis is then given by

θ_f = θ_i + ω_i(t_f - t_i) +  ½α(t_f - t_i)².

These equations are of the same form as the equations for linear motion with constant acceleration a. 
For motion along the x-axis we have

v_f = v_i + a(t_f - t_i),
x_f - x_i = v_xi∆t + ½a_x(t_f - t_i)².

If we replace x by θ and a by α, then the kinematic equations for linear motion along the x-axis transform into the kinematic equations for rotational motion about the z-axis.

With our definitions of angular position, velocity, and acceleration, we have kinematic equations for rotational motions that have the same form as the kinematic equations for translational motion.  And the same equations have the same solutions.  We solve them in exactly the same way.  But the solutions describe different physical situations.  For example, while θ_f can take on any value, a value that does not lie between 0 and 2π radians just tells us that the object has completed more than one revolution.

Problem:

An airliner arrives at the terminal and the engines are shut off.  The rotor of one of the engines has an initial clockwise angular speed of 2000 rad/s.  The engines rotation slows with an angular acceleration of magnitude 80 rad/s².
(a)  Determine the angular speed after 10 s.
(b)  How long does it take the rotor to come to rest?

Solution:

• Reasoning:
  In this problem the initial angular velocity ω_i and the angular acceleration α are given.  If we choose the direction of the initial angular acceleration to be the z-direction, then
  ω_f = ω_i - α(t_f - t_i),
  since α is in the negative z-direction. 
• Details of the calculations
  (a)  At t = 0, ω_i = 2000/s.
  At t = 10 s we have ω_f  = 2000/s - (80/s²)(10 s) = 1200/s.
  (b) Setting ω_f = ω_i - α(t_f - t_i) = 0 we can find the time it takes the rotor to come to rest.
  2000/s - (80/s²)t = 0,  t = (2000/80)s = 25s is the time it takes the rotor to come to rest.

Problem:

A rotating wheel requires 3 s to rotate 37 revolutions.  Its angular velocity at the end of the 3 s interval is 98 rad/s.  What is the constant angular acceleration of the wheel?

Solution:

• Reasoning:
  Given:  Δθ = θ_f - θ_i = 37 revolutions,  Δt = 3 s,  ω_f = 98 rad/s.
  Using θ_f - θ_i = ω_i(t_f - t_i) + ½α(t_f - t_i)² and ω_f = ω_i + α(t_f - t_i), we have two equations, which we can solve for the two unknowns, ω_i and α.
• Details of the calculation:
  Using θ_f = θ_i + ω_i(t_f - t_i) + ½α(t_f - t_i)² with θ_i = 0, we have 37*2π = ω_i*(3 s) + ½α(3 s)².
  Using ω_f = ω_i + α(t_f - t_i) we have 98/s = ω_i + α(3 s).
  We solve this equation for ω_i  ω_i = 98 s - α(3 s), and insert it into the first equation.
  37*2π = (98/s)(3 s) - α(3 s)² + ½α(3 s)², 74π = 294 - α*(9 s²) + α*(4.5 s²),
  (4.5 s²)*α = 294 - 74π, α = 13.67/s² is the constant acceleration of the wheel.

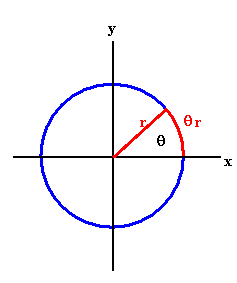When a wheel rotates about the z-axis, each point on the wheel has the same angular speed.  The linear speed v of a point P, however, depends on its distance from the axis of rotation. 
When a point P goes through an angular displacement of 2π, then its distance traveled is 2πr.
When a point P goes through an angular displacement of π, then its distance traveled is πr.
When a point P goes through an angular displacement of θ, then its distance traveled is θr.
In terms of the angular speed ω, the speed v of the point P therefore is v = ωr, if r is constant; v is the tangential velocity of the point P.

External link:  Tangential and angular speed  (Youtube)

The tangential acceleration a of a point P moving along a circular path is given in terms of its angular acceleration by a_t = rα.
The radial or centripetal acceleration is a_r = v²/r = rω².
The total acceleration is given by
a = (a_t² + a_r²)^½ = (r²α² + r²ω⁴)^½ = r(α² + ω⁴)^½.

Problem:

If a car's wheels are replaced with wheels of a larger diameter, will the reading of the speedometer change?  Explain!

Solution:

• Reasoning:
  The sensor for the speedometer senses the angular speed of the wheel.  Using v_nominal = r_nominalω, the speedometer displays the correct speed if the tires have the nominal radius.  If you put larger tires on your car, then your actual speed v_actual = r_actualω is greater than the displayed speed v_nominal = r_nominalω.

Problem:

A car accelerates uniformly from rest and reaches a speed of 22 m/s in 9 s  If the diameter of a tire is 58 cm, find
(a)  the number of revolutions the tire makes during this motion, assuming no slipping, and
(b)  the final rotational speed of the tire in revolutions per second.

Solution:

• Reasoning:
  The uniform acceleration of the car a = Δv/Δt is given.  We can use the kinematic equations for linear motion to find the distance it travels in the time interval Δt.
  Dividing this distance by the circumference of the tire, we find the number of revolution made.  The final angular speed is given by ω_f = v_f/r_tire.
• Details of the calculation:
  (a)  The acceleration of the car is a = Δv/Δt = (22 m/s)/(9 s) = 2.44 m/s².
  The distance traveled in 9 s is d = ½at² = (½*2.44*81) m = 99 m.
  The circumference of the tire is π*0.58 m = 1.82 m.
  The number of revolution made by the wheel is 99/1.82 = 54.3.
  (b)  The final linear speed of the tire is v = 22 m/s.  Using v = ωr, ω = v/r the final angular speed is ω = 75.9/s.  The number of revolutions per second is ω/2π = 12/s.

Embedde Question 1

The kinematic equations for motion with constant linear acceleration and motion with constant angular acceleration have the same form.  Compare motion with constant velocity with motion with constant angular velocity.

Discuss this with your fellow students in the discussion forum!

What causes angular acceleration?

Assume you want to change a rotating wheel's angular speed.  To increase the angular speed you probably will apply a force to the rim, tangential to the rim, and in the direction of the instantaneous velocity of the section of the rim to which you apply the force.

If you want to decrease the angular speed, you will reverse the direction of the force.

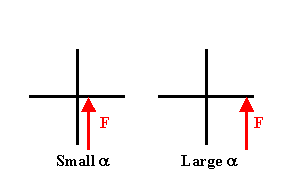Assume you want to enter a building with a rotating door.  The door has four panels, and you push on one of them, perpendicular to the surface of the panel.
The rate, at which the angular velocity of the door changes, i.e. the angular acceleration α, is greater the farther away from the axis of rotation you apply the force.

Angular acceleration about a point is the result of a torque about this point.  A torque is the product of a lever arm and a force that is applied perpendicular to the lever arm.  The lever arm or moment arm is the perpendicular distance from the center of rotation, i.e. from the pivot point, to the point where the force is applied.

A torque is always defined with respect to a pivot point.

A larger torque produces a larger angular acceleration.  You can get a larger torque by applying a larger force, or by using a longer lever arm.  We write

torque = lever arm × force,
τ = r × F.

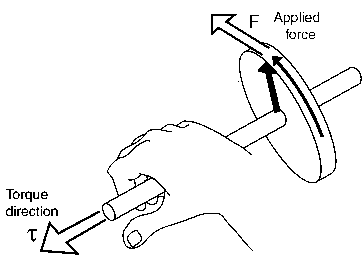Torque is a vector.  It is the vector product or cross product of r and F.  The SI units of torque are Nm.
Torque has magnitude and direction.  Its direction is given by the right-hand rule.

Let the fingers of your right hand point from the axis of rotation to the point where the force is applied.  Curl them into the direction of F.  Your thumb points in the direction of the torque vector.

The magnitude of the torque τ is  τ = rFsinθ, where θ is the smallest angle between the directions of the vectors r and F. 
We can also write τ = r_perpF = rF_perp, where  r_perp is the component of the lever arm perpendicular to F, or where F_perp is the component of F perpendicular to the lever arm.

If a force F acts on an object, then the torque produced by this force about a pivot point is τ = r × F, where r is the displacement vector from the pivot point to the point where the force is applied.  If two or more forces act on an object, then the net torque is the vector sum of the torques produced by the separate forces.  (For rotations about a single axis, two torques can point in the same direction or in opposite directions and therefore can add or subtract.)

Summary

Rotations is the most difficult subject of the course for most students.  The vector nature of the quantities describing rotation is counterintuitive initially, but the math behind rotations is the vector cross product.

Rotation are defined about an axis.  To start an object rotating about an axis, i.e. to give it angular acceleration, you need a force. But not any old force will do.  It depends on where you push or pull, and in which direction.

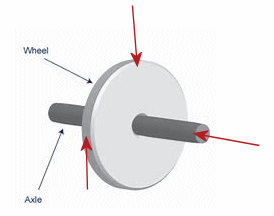
Assume you want to start the wheel spinning.  Let the red arrows indicate the direction of the force you apply.  Which arrow will accomplish this?  You cannot push directly on the axis, that will not work.  You need a lever arm.  You also cannot push towards the axis, even if you have a lever arm.  The force has to have a tangential component.  All this is incorporated in the concept of the torque.

torque = lever arm × force,
τ = r × F.

Here r is the lever arm, pointing from the axis of rotation to the point where the force is applied, F is the force. nThe cross product says that they cannot be aligned because the magnitude of the torque is τ = rFsinθ, where θ is the smallest angle between the directions of the vectors r and F.  The cross product is the mathematical way of expressing what is needed to achieve angular acceleration.

Problem:

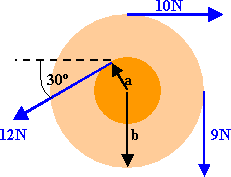
In the figure on the right, find the net torque on the wheel about the axle through the center if a = 10 cm and b = 25 cm.

Solution:

• Reasoning:
  Let the z-axis come out of the page. Use τ = rFsinθ for the magnitude and the right-hand rule for the direction of  τ.
• Details of the calculation:
  The torque produced by the 10 N force then is τ = -(10 N  * 0.25 m) k = -(2.5 Nm) k.
  The torque produced by the 9 N force is τ = -(9 N * 0.25 m) k = -(2.25 Nm) k.
  The torque produced by the 12 N force is τ = (12 N * 0.1 m) k = (1.2 Nm) k.
  (Note that this force is also applied perpendicular to the lever arm.)
  The total torque is τ = -(3.55 Nm) k.

Newton's second law, when applied to rotational motion states that the torque equals the product of the rotational mass or moment of inertia I and the angular acceleration α.

torque = moment of inertia × angular acceleration
τ = Iα

The moment of inertia is a measure of an object's rotational inertia.  It depends on the mass of the object, and on how this mass is distributed with respect to the axis of rotation.  The farther the bulk of the mass is from the axis of rotation, the greater is the rotational inertia (moment of inertia) of the object.  The moment of inertia depends on the mass, and how it is distributed. it does not depend on how much force or torque you apply.  If you apply more torque to a rigid object, you get greater angular acceleration, but the moment of inertia does not change.

The moment of inertia of a system about an axis of rotation can be found by multiplying the mass m_i of each particle in the system by the square of its perpendicular distance r_i from the axis of rotation, and summing up all these products,  I = ∑m_ir_i².

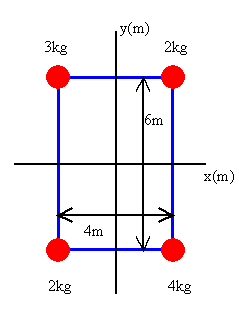Problem:

The four particles in the figure on the right are connected by rigid rods.  The origin is at the center of the rectangle.   Calculate the moment of inertia of the system about the z-axis.

Solution:

• Reasoning:
  The moment of inertia is I = ∑m_ir_i².  Here r_i is the perpendicular distance of particle i from the z-axis.
• Details of the calculation:
  Each particle is a distance r = (9 + 4)^½ m = (13)^½ m from the axis of rotation.
  I = (3 kg + 2 kg + 4 kg + 2 kg)*13 m² = 143 kg m².

The moment of inertia of an object is a measure of its resistance to angular acceleration.  Because of its rotational inertia you need a torque to change the angular velocity of an object.  If there is no net torque acting on an object, its angular velocity will not change.  If it is initially not spinning, it will not start spinning.  If it is spinning with a given angular velocity, this angular velocity will not change.  Both, its angular speed and the orientation of its axis of rotation, will stay the same.

constant angular velocity <--> no angular acceleration <--> no net torque

When two objects are acted on by the same torque, the object with the larger moment of inertia has the smaller angular acceleration.  The units of the moment of inertia are units of mass times distance squared, for example kgm².

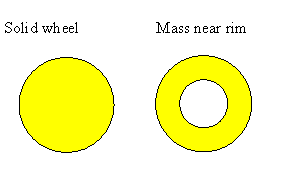
Imagine two wheels with the same mass.  One is a solid wheel with its mass evenly distributed throughout the structure, while the other has most of the mass concentrated near the rim. 

The wheel with the mass near the rim has the greater moment of inertia.

The moment of inertia is defined with respect to an axis of rotation.

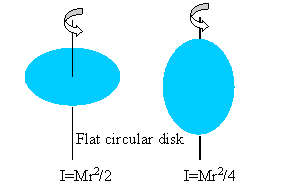For example, the moment of inertia of a circular disk spinning about an axis through its center perpendicular to the plane of the disk differs from the moment of inertia of a disk spinning about an axis through its center in the plane of the disk.

External link:  List of moments of inertia

The seesaw

Two children are playing on a seesaw, rocking back and forth.  The center of the seesaw is fixed.  There is no translational motion.  We observe rotational motion about the center.  While the seesaw is moving there is practically no torque on the seesaw, and it rotates with uniform angular velocity.  The weight of each child times the lever arm from the center to where the child is seated produces a torque, but the two torques have the same magnitude and point in opposite directions and therefore cancel.  If one child is heavier, it sits closer to the center than the lighter child.  This reduces the lever arm.  In this way, different weights can produce torques of the same magnitude.

When one child's feet hit the floor, the floor pushes back and produces a torque pointing opposite to the angular velocity.  This torque will reduce the angular velocity to zero in a short time interval.  The seesaw is now stopped.  The child then pushes off and the ground pushes back.  The direction of the torque stays the same.  The torque produces an angular acceleration which results in an angular velocity pointing opposite to the original direction.  The seesaw reaches its final angular velocity when the child stops pushing.  It now keeps on rotating with constant angular velocity, until the other child's feet hit the floor.