Lab 3

Circuit elements

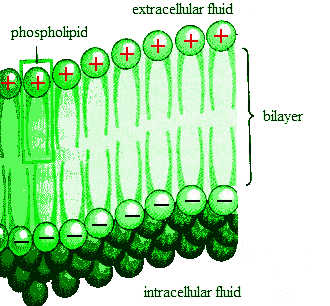Our bodies separate and store charge as a power source to transmit signals along nerves. An excess of positive ions on the outside of the cell membrane results in a potential difference across the membrane. The inside of the cell is at a negative potential of ~100 mV with respect to the outside. The membrane acts like a capacitor.

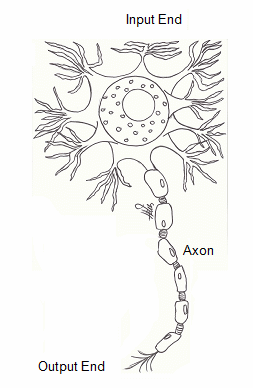
Electrical signals play a role in transmitting information through our bodies. Sensory information is transmitted via nerves. Each nerve consists of a bundle of nerve cells or neurons. A neuron receives stimuli at the input end and produces a signal that is transmitted across the axon to the output end. The axon membrane can be modeled as a charged capacitor. When the neuron is stimulated, the voltage across the capacitor rapidly changes and the charge on the plates reverses, only to thereafter quickly return back to its original value. For this to happen, a current must flow through some effective resistance. The whole axon can be modeled as a chain of capacitors and resistors connected in series and parallel. A voltage and current pulse propagates along this chain.

The speed of propagation of the action potential depends on the electrical resistance R within the core of the axon and the capacitance C across the membrane. A simple electrical circuit, consisting of a resistor in series with a capacitor, has a time constant τ = RC. The time constant characterizes the time it takes for the capacitor to charge and discharge and therefore limits the maximum speed with which signals can travel through the circuit.

In this laboratory you will investigate the behavior of simple circuits containing resistors and capacitors. While you will not model neurons directly, you will become more familiar with how circuits in general behave, and therefore also with how neuron circuits behave.

Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions. This log will become your lab report. Address the points highlighted in blue. Answer all questions.

The resistance of your body

Fatal electric shock occurs when a sufficiently large electric current flows through the body. A fraction of such a current flows through the heart and may disrupt the cardiac cycle. Typical effects are listed in the table below.

Shocking current:	Effect:
<1 mA	no observable effect
~1 mA - ~10 mA	tingling sensation
~10 mA - ~100 mA	muscular paralysis ("can't let go")
~100 mA	ventricular fibrillation
~1A - ~10 A	thermal damage to tissue

Paradoxically, brief currents of > 1 A may be less dangerous than lower currents. Instead of putting the heart into ventricular fibrillation, these currents clamp the whole heart muscle at the same time. When the current is turned off, a normal heart beat may resume on its own accord. Indeed, currents of about 1 A are used clinically to defibrillate the heart.

Experiment 1 (optional)

Do you have a digital multimeter? Then use it to measure the resistance of your body. Switch the meter on the 20 MΩ (or closest) scale. Make sure the leads are plugged into the Ω and COM connectors of the meter. Press the thumb of one of your hands against the black and the thumb of the other hand against the red lead.

Record the measured values with dry and with wet thumbs.

Predict the current that would flow through your body if you held one terminal of a 1.5 V battery in one of your hands and the other terminal in the other hand.
Predict the current that would flow through your body if you held one terminal of a 110 V power source in one of your hands and the other terminal in the other hand.

The salty fluids within the human body are electrical conductors. Salt water conducts electricity because it has mobile electrons and ionic states via the salt atoms. Salt water provides a large surface area of contact for the conductive element and it connects with the sweat glands so electricity can flow past the skin and into your body, which has low electrical resistance. The internal resistance of an arm (from hand to shoulder) is less than 100 Ω. If there is a voltage across this internal resistance, a current will flow and heat will be generated. If the current is large or the connection time is long enough, this heat will cause burns and destroy tissue. Fortunately the resistance of dry skin is high. The dry protein of your skin is an insulator. Using a typical contact area, the skin acts like an approximately (10 - 100) kΩ resistor in series with the internal resistance of the body. At voltages below about 50 V the dry skin provides safe current limiting protection.

If you do not have a digital multimeter, discuss the outcome of this experiment with other students were able to perform this experiment in the discussion forum.

Be extremely careful not to have electrical contact with a voltage source if you have wet or sweaty skin.

DC circuits

Activity 1

Link to the simulation: https://phet.colorado.edu/en/simulations/circuit-construction-kit-dc

Click the Lab icon. Explore the interface!

Components are dragged from the toolbox to make circuits.
To explore the properties of a component, tap it. You can then change many properties and also remove the component.

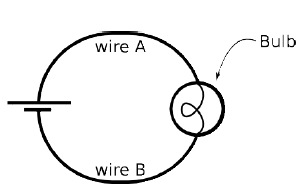(a) Use one ideal battery (40 V, 0 Ω internal resistance), a light bulb (30 Ω) resistance) and ideal wires (near 0 Ω resistance) to build the circuit shown on the right. Make sure your light bulb lights up. Use the voltmeter to measure the potential difference (ΔV) across the battery. Record only the magnitude of the potential difference (omit +/- signs). Make a similar potential difference measurement across the bulb and across each length of wire. With the noncontact ammeter, measure the current through the bulb, I_Bulb.

What to do if you have problems with the animation speed!

Fill in "Table A" below..

ΔV_Battery	ΔV_{wire A}	ΔV_{wire B}	ΔV_Bulb	I_Bulb

Now use two ideal batteries (30 V, 0 Ω internal resistance), three light bulb (30 Ω) resistance) and as many ideal wires as needed to build several different circuits.

(b) Use all the components (two 3 batteries, 3 light bulbs) and connect them in such a way as to they produce the most light. (The largest possible current should flow through the bulbs. You can connect the batteries and bulbs in series or in parallel as needed.)

Make measurements and fill in "Table B" below. Paste a screenshot of your circuit into your word document.

ΔV_Battery	I_Battery	ΔV_{any Bulb}	I_{any Bulb}

(c) Use all the components (two batteries, 3 light bulbs) and connect them in such a way as to they produce the least amount of light or current, but not zero light or current. (The smallest possible non-zero current should flow through the bulbs.)

Make measurements and fill "Table C" below. Paste a screenshot of your circuit into your word document.

ΔV_Battery	I_Battery	ΔV_{any Bulb}	I_{any Bulb}

Set up the circuit shown on the right with three 30 Ω bulbs and one 30 V battery.

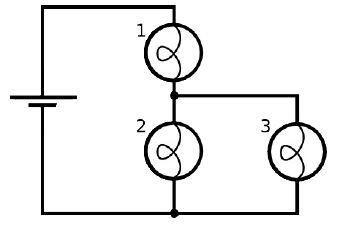
(d) Observe the brightness of the bulbs.

Make measurements and fill in "Table D" below.

ΔV_Battery	I_Battery	ΔV_{Bulb 1}	I_{Bulb 1}	ΔV_{Bulb 2}	I_{Bulb 2}	ΔV_{Bulb 3}	I_{Bulb 3}

(e) Change the internal resistance of the battery to 2 Ω. What happens?

Make measurements and fill in "Table E" below.

ΔV_Battery	I_Battery	ΔV_{Bulb 1}	I_{Bulb 1}	ΔV_{Bulb 2}	I_{Bulb 2}	ΔV_{Bulb 3}	I_{Bulb 3}

Paste Tables A - E into your log and comment on your measurements.

Ohmic and non-ohmic circuit elements

Activity 2

Watch this Youtube video clip discussing resistors.
As far as a circuit is concerned, any device that converts electrical energy into thermal energy is a resistor. But most devices have a more descriptive name, such as hair dryer or heating element, etc. There are devices that are referred to as resistors, primary purpose is the limit the current flowing in a circuit.
Watch this Youtube video clip discussing the resistance of a light bulb.
If a 9 V battery causes the same current to flow through a resistor and a light bulb, both devices dissipate the same power. But the temperature of the resistor barely changes, while the light bulb gets very hot. The resistor has a large surface area and dissipate heat efficiently by conduction and convection in air. The light bulb filament has a small surface area and is in near vacuum. It mainly dissipates heat by radiation. That only becomes efficient at high temperature, because the radiated power is proportional to thr temperature to th 4th power. (Stefan-Boltzmann Law).
Watch this Youtube video clip discussing diodes and LEDs.
Diodes and LEDs ar semiconductor devices with conduction characteristics that can be understood using quantum mechanics but not classical theory.

In a few sentences explain how you can perform and experiment to find out if a circuit element is ohmic or nonohmic. What measurements do you make and how do you decide, based on the results of your measurements.

RC circuits

Activity 3

Link to the simulation: https://phet.colorado.edu/en/simulations/circuit-construction-kit-ac

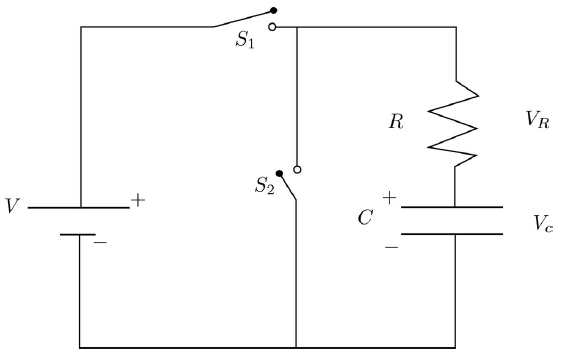
Click the Lab icon. Construct a circuit as shown in the diagram below. Choose R = 50 Ω, C = 0.2 F, V = 9 V.
Use the voltmeter to measure the voltage across the capacitor.

An example is shown below.

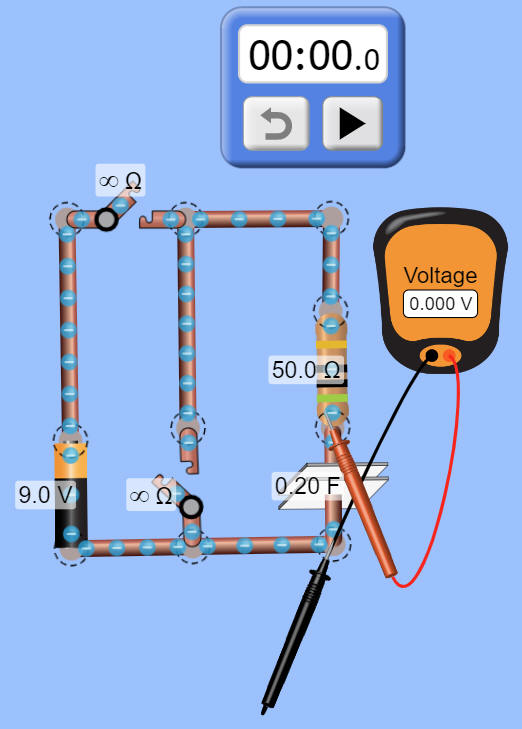
Charging the capacitor:

With the simulation paused, start by clicking on the capacitor to discharge it. The initial voltage across the capacitor should be 0 V.
Click the start button on the stopwatch. The stopwatch will start when you play the simulation. Close switch S₁.

You will monitor the voltage across the capacitor as a function of time as the capacitor in the RC circuit is charging. Start the simulation, then pause it at roughly 0.5 V intervals between 1 V and 8.9 V and record the voltage and time in a table in this spreadsheet.

Paste a screenshot of your circuit into your word document.
Construct a plot of V_c versus t and paste it into your word document. (Make sure you do not switch the axes.)

We expect V_C = V₀(1 - e^-t/τ), where V₀ = 9 V is the battery voltage. We can rewrite this as 1 - V_C/V₀ = e^-t/τ, or ln(1 - V_C/V₀) = -t/τ.
If we plot ln(1 - V_C/V₀) versus time the slope will be -1/τ, where τ is the time constant of the RC circuit.

Add a ln(1 - V_C/V₀) column to your spreadsheet. (The first row with the formula is already filled in.)
Plot ln(1 - V_C/V_O) versus time.
Add a linear trendline, with the intercept set to zero and display the equation on the chart.

Paste it into your word document.
What is your measured time constant of the RC circuit?
How does this compare to the expected time constant τ = RC?
How long does it take to charge the capacitor to V_C = 4.5 V?

Discharging the capacitor:

When the capacitor is fully charged and the voltage across the capacitor is 9V, pause the simulation.
Reset and start the stopwatch.
Open switch S₁ and close switch S₂.
Monitor the voltage across the capacitor as a function of time as the capacitor in the RC circuit is discharging. Start the simulation, then pause it at roughly 0.5 V intervals between 8 V and 0.1 V and record the voltage and time in the spreadsheet.

Construct a plot of V_c versus t and paste it into your word document. (Make sure you do not switch the axes.)
How long does it take to discharge the capacitor to V_C = 4.5 V?

Convert your log into a lab report. See the grading scheme for all lab reports.

Name:
E-mail address:

Laboratory 3 Report

In one or two sentences, state the goal of this lab.
Make sure you completed the entire lab and answered all parts. Make sure you show your work and inserted and properly labeled relevant tables and plots.
Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab3.docx), go to Canvas, Assignments, Lab 3, and submit your document.