Optical instruments

Do you wear glasses?  Are you farsighted or nearsighted?  Look through your or someone else's glasses as you move them towards or away from a printed page.  What do you see?

In the lab you will explore image formation.  You will determine the focal length of a thin lens and observe aberrations.  You will also examine what a camera records when it looks through a simple Keplerian telescope and a simple compound microscope.

Open a Microsoft Word document to keep a log of your procedures, results and discussions.  This log will become your lab report.  Address the points highlighted in blue.  Answer all questions.

Experiment 1

Determine the focal length of a converging lens.

• A diffuse reflecting screen is mounted onto an optical rail.  A laser shines it onto the diffuse reflecting screen from the side as shown in the picture to the right.
  You see a red spot.  This red spot will be the object.  It approximates a point source of light.  Light from the spot can be seen from all directions in front of the screen.
• A converging lens and a mirror are also mounted on the optical rail.  A meter stick is used to determine the positions of the components on the rail.  The screen position is at 0 cm.
• Some of the light from the red spot passes through the lens and then falls on the mirror, where it is reflected.
  If the red spot lies in the focal plane of the lens, then light from the spot will leave the lens as a parallel beam and will be reflected as a parallel beam from the mirror.  If a parallel beam is incident on the lens, it will come to a focus in the focal plane.  This is called the principle of ray reversibility.
  
  
• In the video clip  below the lens is moved along the rail.  Play the video clip in full-screen mode.
  For most lens-screen distances the reflected light does not come to a sharp focus.  But when the lens-screen distances is nearly equal to the focal length of the lens, the reflected spot appears in focus close to the object spot.  (The mirror is slightly tilted so that the reflected spot does not fall exactly on the object spot.)

• Play the video clip.  Pause it when the reflected spot is in focus.  Move the progress bar to different frames until you sure you have found the maximally focused spot.  Measure the distance from the center of the lens to the screen (in units of cm by looking at the position of the lens along the ruler.  That distance is your measured focal length of the lens.  Record your measured focal length in your log.
• Do you think moving the mirror a small distance along the track changes anything?

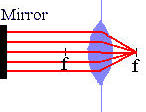
Observe coma.

• In the video clip below the reflected light comes to a reasonably sharp focus when it enters the lens parallel to its symmetry axis.  Then the lens is rotated by approximately 20 degrees about the vertical axis.

• Watch the video clip in full-screen mode.  Describe what happens to the reflected spot.  You should observe a lens aberration called "coma".  It is observed when the light rays make large angles with the symmetry axis of spherical mirrors or lenses.

Experiment 2

Observe the formation of a real image by a converging lens.

• A lamp is mounted 50 cm away from the screen on the optical rail.  A cross pattern is cut into the lamp cover.  The cross faces the screen.  A lens can be moved along the rail to different positions between the lamp and the screen.
   

• In the video clip below the lens is moved along the rail.  Watch the clip in full-screen mode.   Pause it and move the progress bar to the frame where you get the sharpest images of the cross on the screen.

• Measure the object distance x_o from the cross on the lamp to the center of the lens and the image distance x_i from the center of the lens to the image on the screen and record these distances in table 1.
• Note if the image is upright or inverted.
• Using the lens equation,
  1/x_o + 1/x_i = 1/f  of f = x_ox_i/(x_o + x_i),
  calculate the focal length and record it in table 1.
• There are two locations for the lens where you get a sharp image.  Move the lens until you find the second location.  Repeat the measurements and calculations from above and record them in table 1.

Table 1

• Paste the table into your Word document.

For the measurements of experiment 1 and 2 answer the following questions.

• Do the two measurements from experiment 2 yield the same focal length within experimental uncertainties?
  Explain how the measurements could be "off", given the way you measured the focal length.
• Does the focal length obtained in experiment 1 agree with the focal length obtained in experiment 2 within estimated experimental uncertainties?
• In experiment 2, did you observe inverted or upright images?
• Did you observe aberrations?

Simulation 1:

Open the "Lenses" simulation.

You can determine the effective focal length of a bi-convex and two plano-convex lenses.  The object is a parallel beam (representing a point source at infinity).  You can vary the aperture size by varying the beam radius.  Use the mouse to move the lens and the screen along an optical rail and to zoom and rotate the view.  The major unit of the scale on the track is cm.  For large apertures, look for spherical aberrations and observe coma and astigmatism as you rotate the lens.  For some lenses coma is the dominant aberration, while for others it is astigmatism.

(a)  Choose a beam radius of ~ 0.7 cm and a lens rotation of zero. In succession, choose lens # 1 - 4.  These are not necessarily thin lenses.  Determine the effective focal length of each lens by bringing the parallel laser beam to a focus on the screen.  Varying the distance between the lens and screen until the best focus is achieved.

Fill in the table below.

Table 2

• Paste your table into your log. 

• Does it matter which side of lens 3 is facing the beam?

(b)  Observe coma.
Choose lens 2 and put the screen in its focal plane.  Rotate the lens by ~ 30 degrees in either direction. 

• Describe your observation. 
• Zoom in on the screen and insert a screen capture in your log.

Simulation 2:

Open the "Images" simulation.

You can also determine the effective focal length of a bi-convex and two plano-convex lenses by using a lamp with markings as the object.  Use the mouse to move the lamp, lens, and the screen along an optical rail and to zoom and rotate the view. The major unit of the scale on the track is cm.  For large apertures, look for spherical aberrations and observe coma and astigmatism as you rotate the lens.

(a)  Choose lens 2, an aperture size of 0.7 cm and a lens rotation of 0.  Place the lamp 9 cm in front of the lens and move the screen until you find the sharpest image.  Measure the image distances.  Calculate the focal length of lens 2 from f = x_ox_i/(x_o + x_i). 

• Record the measured object distance, image distance and focal length in your log.
• Does The focal length agree with the focal length of lens 2from table 2?
• What happens as you change the aperture size?  Do you have to move the screen to get a sharper image?
  (Review spherical aberrations and the circle of least confusion.)

Observation 1

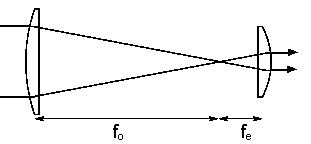A simple Keplerian telescope with a magnifying power of ~3.1 is mounted on the optical rail.
It uses 12.5 cm focal length lens for the objective and the 4 cm focal length lens for the eyepiece. 
The center to center distance between the lenses be ~16.5 cm.

The telescope is pointed at a book sitting standing on a cart near a door across the room.  The camera looks through the eyepiece and takes a picture.  The lens of the camera produces a real image at the location of the camera sensor.  The picture on the left is taken with the camera in the same position and the telescope moved to the side.

    

• Describe features of the image (orientation, aberrations).

Observation 2

A (very poorly designed) simple compound microscope with a tube length g of 16 cm, an objective with focal length f_o = 6 cm, and an eyepiece with focal length 12.5 cm is mounted on an optical rail.  16 cm is the most common tube length for laboratory microscopes.  The center to center distance between the lenses be 34.5 cm.  The target is placed ~8.5 cm in front of the objective.  The magnifying power of this microscope, when the human eye is used as the detector, is MP = -(g/f_o)(25 cm/f_e) ~ 5.3.  Here the camera is used as a detector.  The camera lens is positioned close to the eyepiece and moved and forms a reasonably sharp image of the object on the camera sensor.

Schematic and picture of the simple compound microscope.

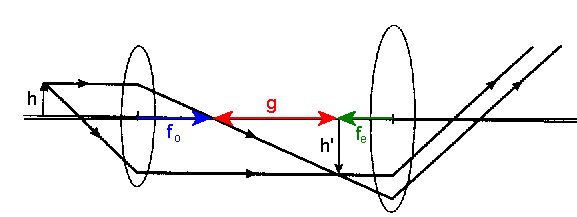
Below you see the image of the target produced by the camera lens.  The eyepiece lens is large, there is no actual tube, and the camera lens has a wide acceptance angle, so the camera can "look around" the objective. The picture on the left is taken with the camera in the same position and the microscope moved to the side.

     

• Describe features of the image (orientation, aberrations).  To decide on the orientation, look at the image of another target below.  (Here "square" is the word.)

       

Convert your log into a lab report.  See the grading scheme for all lab reports.

Name:
E-mail address:

Laboratory 8 Report

• In one or two sentences, state the goal of this lab.
• Make sure you completed the entire lab and answered all parts.  Make sure you show your work and inserted and properly labeled relevant tables and plots.
• Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab8.docx), go to Canvas, Assignments, Lab 8, and submit your document.