Lab 8
All waves diffract, if they pass through or around obstacles, and interfere, if two or more waves arrive at the same place at the same time. When a monochromatic plane wave passes through a single slit of width w, we observe a Fraunhofer single slit diffraction pattern a large distance L >> w away from the slit. When the wave passes through multiple regularly-spaced slits with slit-spacing d, we observe a multiple-slit Fraunhofer interference pattern a large distance L >> d away from the slits.
Light is an electromagnetic wave. You will use a simulation to observe a He-Ne laser beam (λ = 633 nm) to produce diffraction and interference pattern. You will use these patterns to measure the width of a single slit and a hair and the spacing of two slits.
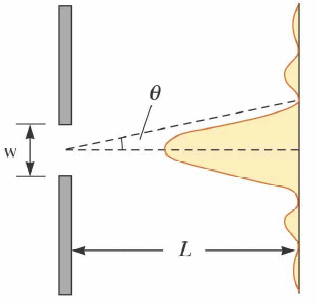 When monochromatic light from a distant source passes
through a narrow slit of width w in an opaque mask we observe a
diffraction pattern on a distant
screen. The pattern is characterize by a central maximum and
alternating dark and bright fringes, which appear symmetrically in both
sides of the central maximum. The central maximum is twice as
wide, and much brighter than the other bright fringes.
When monochromatic light from a distant source passes
through a narrow slit of width w in an opaque mask we observe a
diffraction pattern on a distant
screen. The pattern is characterize by a central maximum and
alternating dark and bright fringes, which appear symmetrically in both
sides of the central maximum. The central maximum is twice as
wide, and much brighter than the other bright fringes.

The dark fringes in the diffraction pattern of a single slit are found at angles θ for which w sinθ = mλ, where λ is the wavelength of the light and m is an integer, m = 1, 2, 3, ... .
If light with wavelength λ passes through two or more slits separated by equal distances d, we will observe interference fringes inside the single slit diffraction pattern. At certain angles we observe constructive interference. These angles are found by applying the condition for constructive interference, which is
d sinθ = mλ, m = 0, 1, 2, ....
We will only see the bright interference fringes, if they do not appear at the angle θ of a diffraction minimum. If d sinθ = mλ = w sinθ, then the bright fringe of order m will be missing. Look again at this picture!
Open a Microsoft Word document to keep a log of your procedures. This log will become your lab report. Address the points highlighted in blue. Answer all questions.
Part 1: Observe and analyze a single slit and multiple slit diffraction patterns
In the simulation a He-Ne laser beam (λ = 633 nm) produces Fraunhofer diffraction and
interference pattern that you can observe on a screen. A mouse is required
to interact with the simulation. It does not respond to touch. You can drag four
different slides into the the of the laser beam, and you can vary the slide to
screen distance. Clicking anywhere on the breadboard you can rotate and
zoom the view. The screen and the slides snap to the holes on the
breadboard which have a spacing of 1 unit = 2.5 cm. The screen is 4 units
wide and 2 units high and the lines on the screen are spaced by ½ unit.
Three of the slides block all the light except for a
single w = 20 μm wide slit or two or four w = 20 μm wide slits with slit
spacing d. From the observed patterns you can verify the slit width w and
determine the slit spacing d. The only thing blocking the laser light on a
fourth slide is a hair. You can measure the width of the hair using the
diffraction pattern produced by the laser light.
The lines on the slides are not drawn to scale. Their purpose is just to identify the slides. The most intense regions of the diffraction and interference patterns always have the same maximum color intensity allowed by the computer graphics. A realistic decrease in the color intensity with distance from the slit(s) would make the dimmer regions of the diffraction and interference patterns invisible at larger distances. That is a limitation of the computer graphics.
Click on the image to open the app!
(a) Drag the single slit slide into into the path of the laser beam.
The slit width w is 20 μm. Observe the diffraction pattern.
Dark fringes in the diffraction pattern of a single slit are found at angles θ
for which w sinθ = mλ, m = 1, 2, ... .
To see a well-resolved pattern, use a large distance between the slit and the
screen.
- Verify the slit width w. There are several measurements you can make. Pick one. Explain which measurement you made and show a screenshot, your calculation, and your result for the slit width.
(b) Drag the double slit slide into into the path of the laser beam. Each slit is w is 20 μm wide. Constructively interference at angles θ such that d sinθ = mλ, m = 0, 1, 2, ... .
- Determine the slit spacing d. There are several measurements you can make. Pick one. (Hint) Explain which measurement you made and show a screenshot, your calculation, and your result for the slit spacing.
(c) Drag the slide with four slits into into the path of the laser beam. Again each slit is w = 20 μm wide.
- As you observe the pattern, does it differ from that of the double slit for the same slide to screen distance L? If yes, what is different? (Zoom in to get a better view.)
Part 2: Measure the thickness of a hair
The dark fringes in the diffraction pattern of a single slit are found at angles θ for which w sinθ = mλ, where λ is the wavelength of the light and m is an integer, m = 1, 2, 3, ... .
 The intensity at the screen is proportional to the
square of the electric field amplitude.
The intensity at the screen is proportional to the
square of the electric field amplitude.
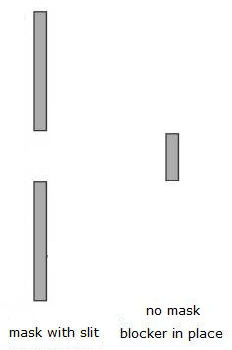
- If we block the slit completely with an opaque blocker, the electric field at a large distance is zero.
- If we remove mask with the slit, the electric field at a large distance is that of the non-diffracted beam.
What if we remove the mask and only leave the blocker of width w? Using Huygens' principle we have
Emask with slit + Eblocker (no mask) = Enon-diffracted beam.
Here Emask with slit is the field
produced by sources at locations of the mask and Eblocker
(no mask) is the field produced by source at locations of the
blocker.
Therefore
Eblocker (no mask) = Enon-diffracted beam - Emask with slit.
For a laser beam the divergence angle θ0 is small, and for angles θ > θ0 we have
Eblocker (no mask) = - Emask with slit.
For angles θ > θ0 the average intensity, which is proportional to the square of the electric field, therefore is the same as that for the single slit. Dark fringes in the diffraction pattern are found at angles θ for which w sinθ = mλ.
Drag the slide with the hair into into the path of the laser beam.
- Observe the diffraction pattern on the screen. Determine the diameter w of the hair. plain which measurement you made and show a screenshot, your calculation, and your result for the diameter of the hair.

You can do this experiment at home and determine the thickness of your own hair if you have a laser pointer and you know the wavelength of the light. For most red laser pointers λ = 650 nm = 0.65 μm, and for most green laser pointers λ = 532 nm = 0.532 μm.
- Cut a hole into an index card and tape a hair across the hole. Make sure the hair is stretched out and you can mount it vertically.
- Mount the index card, for example by folding it and sticking the folded end between the pages of a book.
- Observe the diffraction pattern on another index card a distance L from the hair. It is best to cut a slit into the second card and
let the direct beam pass through the slit, because the direct beam is very
bright. It is easier to observe the diffraction pattern without the
very bright spot in the middle.

- Make the appropriate distance measurements and solve w sinθ = mλ for the hair diameter w.
