What are the constituents that make up the world around us and how do they interact?

As physicists, we observe, we experiment, and we build conceptual models.  We build models on many different levels.  Models are made by people for people.  A model is a manageable representation of the underlying reality.  Models can change as our knowledge changes, but the underlying reality presumably does not change. 

Different physical models have different ranges of applicability, they have been verified to work on different scales.

Examples of scales:

Cosmic	Material	Atomic and Nuclear	Elementary Particle

The science of Physics is often divided into Classical Physics and Modern Physics.

Classical Physics in a model of the macroscopic world around us.  All the laws of classical physics were known by the end of the 19^th century.  Classical physics works well describing and predicting almost all everyday phenomena.  The known properties of matter at the end of the 19th century were mass and charge.  The smallest constituents were atoms.  The known interactions were gravity, modeled by Newton's law of gravitation, electromagnetic interactions, modeled by Maxwell's equations, and contact force arising from the requirement that "atoms need their space".
Consequences of the interactions were described by Newton's laws of motion, which predict how matter behaves when acted on by forces.  Statistical physics and thermodynamics were developed for describing systems with a large number of degrees of freedom.

Modern Physics is the physics of the 20^th century.  The main building blocks, the theory of relativity and quantum mechanics, were developed early in that century.  Two different types of problems with classical physics became obvious at the end of the 19th century.  One problem was an internal inconsistency.  The other type of problem arose from measurements that could not be understood using classical physics.

Special relativity

Maxwell' equations predict that the speed of light in free space is c = 3*10⁸ m/s.  They do not specify a reference frame.  In physics, however, speed is defined with respect to a reference frame. 

Example:

You walk from the back to the front of the airplane with a speed of 1 m/s relative to the plane.   The airplane is flying with a speed of 200 m/s in the forward direction with respect to the surface of Earth.  Your speed with respect to the surface of Earth is 201 m/s.

You send a pulse of light from the back to the front of the airplane.  Maxwell's equations predict the speed of that pulse to be c with respect to the airplane and with respect to the surface of the earth.  What gives?

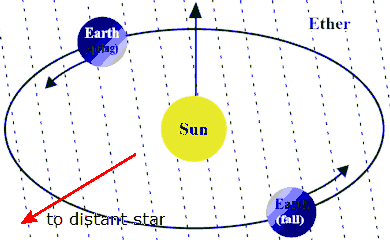
The first inclination of physicists was to assume that even though Maxwell did not specify a reference frame in which light moved with speed c, such a unique reference frame surely had to exist.  It was called the ether, some type of substance that permeated all space, and through which light waves propagated with speed c.  Experiments were looking for this ether, but never found it.  A famous experiment, called the Michelson-Morley experiment, used an interferometer to make high-precision measurements of the speed of light emitted by a distant star with respect to Earth.  Measurements were made at different times of the year, when Earth was moving towards or away from the star in its orbit around the sun.  The Michelson-Morley experiment found no dependence of the speed of light with respect to Earth on the time of the measurement and is often cited as the definite experiment disproving the existence of the ether. 

Einstein special theory of relativity resolves the conflict between Newton's laws of motion and Maxwell's equations.  Einstein proposed two postulates.

I. The laws of nature are the same in all inertial reference frames.
II. In vacuum, light propagates with respect to any inertial frame and in all directions with the universal speed c. This speed is a constant of nature.

In order to satisfy both postulates the ideas of absolute time and space had to be abandoned.  Depending on their state of motion, different observers will measure different space and time intervals between events.  The differences become only apparent when the relative speed of the observers approaches the speed of light.  Newton's laws of motion still hold, as long as the second law is written as F = ∆p/∆t.

• The momentum of a particle of mass m however has to be redefined. 
• The relativistically correct momentum is p = γmv, with  γ = 1/(1 - v²/c²)^½ = (1 - v²/c²)^-½.
• As long as speed of the particle is much smaller than c, p ≈ mv.
• The expression for the total energy of a particle also changes.
• The total relativistic energy of a particle of mass m is written as the sum of its mass energy mc², its kinetic energy KE, and its potential energy PE.
• For a free particle with zero potential energy the total energy can be written as
  E = (m²c⁴ + p²c²)^½ = γmc².
• When the kinetic energy is small compared to the rest energy, both expressions can be simplified, yielding the mass energy and the non-relativistic expression for the kinetic energy.
  E = mc² + p²/(2m) = mc² + ½mv².

Relativistic corrections to the equations of motions become important when the speed of a particle approaches the speed of light, or when its kinetic energy becomes comparable its the rest energy.  The relativistic energy formula must be used to analyze fast collisions, particle creation, particle annihilation, and particle decay.