 Atoms make up
ordinary matter. In 1897 J. J. Thomson discovered the electron, a
negatively charged particle more than two thousand times lighter than a
hydrogen atom. In 1906 Thomson suggested that each atom
contained a number of electrons roughly equal to its atomic number.
Since atoms are neutral, the charge of these electrons must be balanced
by some kind of positive charge. Thomson proposed a 'plum pudding'
model, with positive and negative charge filling a sphere ~10-10 meter across. This plum pudding model was generally
accepted. Even Thomson's student Rutherford, who would later prove the
model incorrect, believed in it at the time.
Atoms make up
ordinary matter. In 1897 J. J. Thomson discovered the electron, a
negatively charged particle more than two thousand times lighter than a
hydrogen atom. In 1906 Thomson suggested that each atom
contained a number of electrons roughly equal to its atomic number.
Since atoms are neutral, the charge of these electrons must be balanced
by some kind of positive charge. Thomson proposed a 'plum pudding'
model, with positive and negative charge filling a sphere ~10-10 meter across. This plum pudding model was generally
accepted. Even Thomson's student Rutherford, who would later prove the
model incorrect, believed in it at the time.
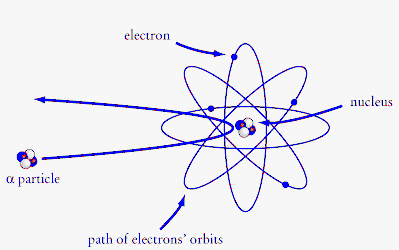 But
in 1911 Ernest Rutherford proposed that each atom has a
massive nucleus containing all of its positive charge, and that the much
lighter electrons are outside this nucleus. The nucleus has a
radius about ~ 10-14 - 10-15 m, ten thousand to one hundred thousand times smaller than the radius
of the atom. Rutherford arrived at this model by doing experiments.
He scattered alpha particles off fixed targets and observed some of them
scattering through very large angles. Scattering at large angles
occurs when the alpha particles come close to a nucleus. The
reason that most alpha particles are not scattered at all is that they
are passing through the relatively large 'gaps' between nuclei.
But
in 1911 Ernest Rutherford proposed that each atom has a
massive nucleus containing all of its positive charge, and that the much
lighter electrons are outside this nucleus. The nucleus has a
radius about ~ 10-14 - 10-15 m, ten thousand to one hundred thousand times smaller than the radius
of the atom. Rutherford arrived at this model by doing experiments.
He scattered alpha particles off fixed targets and observed some of them
scattering through very large angles. Scattering at large angles
occurs when the alpha particles come close to a nucleus. The
reason that most alpha particles are not scattered at all is that they
are passing through the relatively large 'gaps' between nuclei.
Links:
(animations)
The Rutherford Experiment
Thomson Model of an Atom
Rutherford Model
Rutherford revised Thomson's 'plum pudding'
model, proposing that electrons orbit a positively charged nucleus, like
planets orbit a star. But orbiting particles continuously
accelerate, and accelerating charges produce electromagnetic radiation.
According to classical physics the planetary atom cannot exist.
Electrons quickly radiate away their energy and spiral into the nucleus.
In 1915 Niels Bohr adapted Rutherford's model by saying that the orbits
of the electrons were quantized, meaning that they could exist only at
certain distances from the nucleus. Bohr proposed that electrons
did not emit electromagnetic radiation when moving in those quantized orbits.
What do our instruments reveal today? Here are 3 examples.
All the examples reveal the probability distribution of atomic electrons,
i.e. the probability of finding an electron at certain positions near an atomic
nucleus.
The field ion microscope and the STM look at atomic cores that are fixed in the
crystal structure of a conductor. By different means they supply barely
enough energy to remove the electron from the conductor's surface The
electron is most likely removed from positions near the atomic cores. The
removed electron is replaced by a small current flowing to the ground. So
electrons can be repeatedly removed from the same atoms and plotting the number
of electrons removed or the current flowing versus position maps the electron
probability distribution.
The quantum microscope works with a beam of atoms. Electrons are
removed from different, identically prepared atoms. A electron optics
system images their removal position onto a detector. Each atom only
contributes one electron. but after a sufficient number of electrons has
been detected, a very detailed probability distribution emerges.,

Quantum microscope peers into the H atom
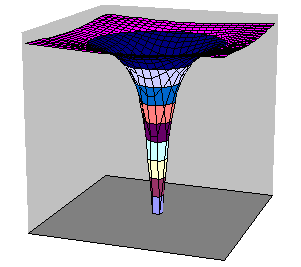 Quantum mechanics now predicts what measurements can reveal about atoms.
The hydrogen atom represents the simplest possible atom, since it consists of
only one proton and one electron. The electron is bound, or confined.
Its potential energy function U(r) expresses its electrostatic potential energy
as a function of its distance r from the proton.
Quantum mechanics now predicts what measurements can reveal about atoms.
The hydrogen atom represents the simplest possible atom, since it consists of
only one proton and one electron. The electron is bound, or confined.
Its potential energy function U(r) expresses its electrostatic potential energy
as a function of its distance r from the proton.
U(r) = -qe2/(4πε0r).
In SI unit 1/(4πε0) = 9*109 Nm2/C2,
and qe = 1.6*10-19 C.
The figure on the right shows the shape of U(r) in a plane containing
the origin. The potential energy is chosen to be zero at infinity.
The electron in the hydrogen atom is confined in the potential well, and
its total energy is negative.
Confinement leads to energy quantization.
The allowed energies of the electron in the hydrogen atom are
En = -13.6 eV/n2.
Here n is called the principle quantum
number. The values En are the possible value
for the total electron energy (kinetic and potential energy) in the
hydrogen atom. The average potential energy is -2*13.6 eV/n2
and the average kinetic energy is +13.6 eV/n2. The electron has four degrees of freedom, the three
spatial degrees of freedom and one internal degree of freedom,
called spin. To completely determine its initial wave function,
we, in general, have to make four compatible measurements.
Some observables that are compatible with energy measurements and
compatible with each other are
- the magnitude of the electron's orbital angular momentum,
labeled by the quantum number l,
L = (l(l + 1))1/2ħ,
- the projection of the electron's orbital angular momentum along
one axis, for example the z-axis, labeled by the
quantum number m,
Lz = mħ,
- and the projection of the electron's spin along one axis,
labeled by by the quantum number ms,
Sz = msħ.
We can know the values of these observables, labeled by
n, l, m, and ms, simultaneously.
For the hydrogen atom, the energy levels only depend on the principal quantum number n. The energy levels are
degenerate, meaning that the electron in the hydrogen atom can be in
different states, with different wave functions, labeled by a different
set of quantum numbers, and still have the same energy.
The electron wave functions however are different for every different set of quantum numbers.
- For each principal quantum number n, all smaller positive
integers are possible values for the quantum number l, i.e.
l = 0, 1, 2, ..., n - 1.
The quantum number l is always smaller than
the quantum number n. Only states with high energy can
have large angular momentum.
- The quantum number m can take on all
integer values between -l and l.
Examples of hydrogen atom probability densities.
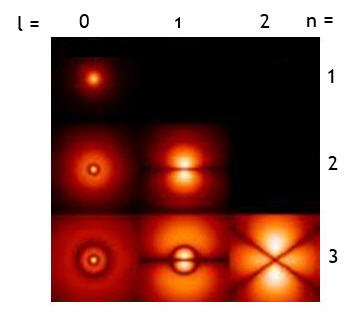 |
As n increases,
the number of
radial nodes increases.
As l increases,
the number of
angular nodes increases. |
 |
- The principal quantum number "n" of an electron in an atom
is primarily used
to identify the main energy level or shell.
- The angular momentum quantum number "l" of an electron in an atom
is primarily
used to determine the shape of the orbital.
- The "magnetic" quantum number "m" of an electron in an atom
is primarily used to determine the orientation of the orbital.
|
Note: Energy eigenfuctions characterize
stationary state. We cannot track the electron and know its energy
at the same time. If we know its energy, we can only predict
probabilities for where we might find it if we tried to measure its
position. If we determine the position of the electron, we lose
the energy information.
| l = 1 |
s |
| l = 2 |
p |
| l = 3 |
d |
| l = 4 |
f |
| l = 4 |
g |
Often texts use a different notation to refer to the
energy levels of the hydrogen atom. Letters of the alphabet are associated with various values of l.
| Spectroscopic notation |
Quantum number n
of the state |
Quantum number l
of the state |
Possible values of
the quantum number m |
|
1s
|
1
|
0
|
0
|
|
2s
|
2
|
0
|
0
|
|
2p
|
2
|
1
|
-1, 0, 1
|
|
3s
|
3
|
0
|
0
|
|
3p
|
3
|
1
|
-1, 0, 1
|
|
3d
|
3
|
2
|
-2, -1, 0, 1, 2
|
|
4s
|
4
|
0
|
0
|
|
4p
|
4
|
1
|
-1, 0, 1
|
|
4d
|
4
|
2
|
--2, -1, 0, 1, 2
|
|
4f
|
4
|
3
|
-3, -2, -1, 0, 1, 2, 3
|
The hydrogen line spectrum
 When an electron changes from one energy level to
another, the energy of the atom must change as well. It requires
energy to promote an electron from a lower energy level to a higher one.
This energy can be supplied by a photon whose energy E is given in terms
of its frequency E = hf or wavelength E = hc/λ.
When an electron changes from one energy level to
another, the energy of the atom must change as well. It requires
energy to promote an electron from a lower energy level to a higher one.
This energy can be supplied by a photon whose energy E is given in terms
of its frequency E = hf or wavelength E = hc/λ.
Since the energy
levels are quantized, only certain photon wavelengths can be absorbed.
If a photon is absorbed, an electron will be promoted to a higher energy
level and will then fall back down into the lowest energy state (ground
state) in a cascade of transitions. Each time the energy level of
the electron changes, a photon will be emitted and the energy
(wavelength) of the photon will be characteristic of the energy
difference between the initial and final energy levels of the atom in
the transition. The energy of the emitted photon is just the
energy difference between the initial (ni) and
the final (nf) state.
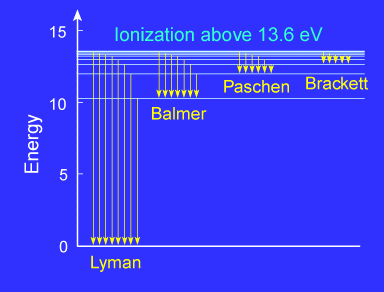
The set of spectral lines for a given final state nf are
generally close together. In the hydrogen atom they are given
special names. The lines for which nf = 1 are called the
Lyman series. These transitions frequencies correspond to spectral
lines in the ultraviolet region of the electromagnetic spectrum.
The lines for which nf = 2 are called the
Balmer series and
many of these spectral lines are visible. The spectrum of hydrogen
is particularly important in astronomy because most of the Universe is
made of hydrogen. The Balmer series, which is the only hydrogen series
with lines in the visible region of the electromagnetic spectrum, is
shown in the right in more detail.
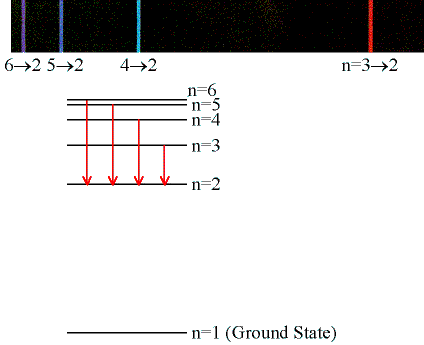 The Balmer lines are designated by H with a Greek subscript in order of decreasing
wavelength. Thus the longest wavelength Balmer transition is designated
H with a subscript alpha, the second longest H with a subscript beta,
and so on.
The Balmer lines are designated by H with a Greek subscript in order of decreasing
wavelength. Thus the longest wavelength Balmer transition is designated
H with a subscript alpha, the second longest H with a subscript beta,
and so on.

Problem:
What is the wavelength of the least energetic line in the Balmer
series?
Solution:
- Reasoning:
The transition from ni = 3 to nf = 2
is the lowest energy, longest wavelength transition in the Balmer series.
- Details of the calculation:
∆E = -13.6 eV(1/9 - 1/4) = 1.89 eV =
3*10-19 J. λ = hc/∆E = 656
nm.
Problem:
What is the shortest wavelength in the Balmer series?
Solution:
- Reasoning:
The transition from ni = ∞ to nf = 2
is the highest energy, shortest wavelength transition in the Balmer series.
- Details of the calculation:
∆E = -13.6 eV(1/∞ - 1/4) = 13.6/ 4 eV =
3.4 eV = 5.44*10-19 J. λ = hc/∆E
= 365 nm.
Problem:
Do the Balmer and Lyman series overlap? To answer this,
calculate the shortest-wavelength Balmer line and the longest-wavelength Lyman
line.
Solution:
- Reasoning:
From the previous problem we know that the shortest-wavelength Balmer line
has λ = 365 nm.
The transition from ni = 2 to nf = 1
is the lowest energy, longest wavelength transition in the Lyman series.
- Details of the calculation:
∆E = -13.6 eV(1/2 - 1) = 13.6/ 2 eV
= 6.8 eV. λ = hc/∆E
= 182 nm.
The two series do not overlap.
Embedded Question 1
- Hydrogen gas can only absorb EM radiation that has an energy
corresponding to a transition in the atom, just as it can only emit these
discrete energies. When a spectrum is taken of the solar corona, in
which a broad range of EM wavelengths are passed through very hot hydrogen
gas, the absorption spectrum shows all the features of the emission
spectrum. But when such EM radiation passes through
room-temperature hydrogen gas, only the Lyman series is absorbed.
Explain the difference.
Discuss this with your fellow students in the discussion forum!
Hydrogenic atoms
Atoms with all but one electron removed are called
hydrogenic atoms.
- If the charge of the nucleus is Z times the proton charge,
then U(r) = -Zqe2/(4πε0r).
- The energy levels of such atoms are obtained by simply
scaling the the solutions for the hydrogen atom.
The energy levels scale with Z2, i.e. En = -Z2*13.6
eV/n2. It takes more energy to remove an electron
from the nucleus, because the attractive force that must be overcome is
stronger.
- The average size of the wave functions scales as 1/Z, i.e.
the electron, on average, stays closer to the nucleus, because the
attraction is stronger.
Problem:
Atoms can be ionized by thermal collisions, such as at the high
temperatures found in the solar corona. One such ion is C+5 , a
carbon atom with only a single electron.
(a) By what factor are the energies of its hydrogen-like levels greater than
those of hydrogen?
(b) What is the wavelength of the first line in this ion's Paschen series?
(c) What type of EM radiation is this?
Solution:
- Reasoning:
The energy levels of hydrogenic atoms scale with Z2, the wave
functions scales as 1/Z.
- Details of the calculation:
(a) The charge of the carbon nucleus is 6 times the proton charge.
All energy level increase by a factor of Z2 = 36.
(b) λ = hc/∆E, all
wavelengths of the Paschen series of carbon decrease by a factor of 36
compare to the corresponding wavelengths of hydrogen.
For hydrogen the first line of the Paschen series has
∆E = -13.6 eV(1/16 - 1/9) = 0.66 eV, λ = hc/∆E
= 1876 nm.
For carbon the first line of the Paschen series has λ = hc/∆E
= 1875/36 nm = 52.1 nm.
(c) This is far UV radiation.
The Bohr Atom
In 1913 Bohr's model of the atom revolutionized atomic physics. The Bohr model consists of four principles:
- Electrons assume only certain orbits around the nucleus. These orbits
are stable and called "stationary" orbits. Electrons in these orbits do not
radiate their energy away.
- Each orbit is associated with a definite value of the energy and the
angular momentum. Bohr assumed that the angular momentum could only take on
values that were integer multiples of ħ.
Angular momentum = mr2ω = mrv = nħ, n = 1, 2, 3, ... .
A classical electron with a definite angular momentum in an orbit about a
proton also has a definite energy E .
If angular momentum = mrv = nħ, then En = -me4/(2ħ2n2)
= -13.6 eV/n2.
The orbit closest to the nucleus has an energy E1, the next
closest E2 and so on.
A definite angular momentum also implies a definite orbital radius.
If angular momentum = mrv = nħ, then rn = n2ħ2/(me2)
= n2a0 = n2 * (52.92 pm).
a0 is called the Bohr radius.
- A photon is emitted when an electron jumps from a higher energy orbit to
a lower energy orbit and absorbed when it jumps from a lower energy orbit to
higher energy orbit. The photon energy is equal to the energy difference
∆E = hf = Ehigh - Elow.
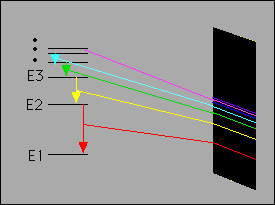 With these conditions Bohr was able to explain the
stability of atoms, as well
as the emission spectrum of hydrogen. According to Bohr's model only certain
orbits are allowed, which means only certain energies are possible. These
energies naturally lead to the explanation of the hydrogen atom spectrum.
With these conditions Bohr was able to explain the
stability of atoms, as well
as the emission spectrum of hydrogen. According to Bohr's model only certain
orbits are allowed, which means only certain energies are possible. These
energies naturally lead to the explanation of the hydrogen atom spectrum.
Bohr's model was so successful that he immediately received
world-wide fame. Unfortunately, Bohr's model worked only for hydrogen and hydrogenic atoms, such as any atom with all but one electron removed.
The Bohr model is easy to picture, but we now know that it is wrong. Any planetary model of the atom, so often
seen in pictures and so easy to picture, is wrong. Energy and
position are incompatible observables. We cannot track an electron with a
known energy inside an atom.
 Atoms make up
ordinary matter. In 1897 J. J. Thomson discovered the electron, a
negatively charged particle more than two thousand times lighter than a
hydrogen atom. In 1906 Thomson suggested that each atom
contained a number of electrons roughly equal to its atomic number.
Since atoms are neutral, the charge of these electrons must be balanced
by some kind of positive charge. Thomson proposed a 'plum pudding'
model, with positive and negative charge filling a sphere ~10-10 meter across. This plum pudding model was generally
accepted. Even Thomson's student Rutherford, who would later prove the
model incorrect, believed in it at the time.
Atoms make up
ordinary matter. In 1897 J. J. Thomson discovered the electron, a
negatively charged particle more than two thousand times lighter than a
hydrogen atom. In 1906 Thomson suggested that each atom
contained a number of electrons roughly equal to its atomic number.
Since atoms are neutral, the charge of these electrons must be balanced
by some kind of positive charge. Thomson proposed a 'plum pudding'
model, with positive and negative charge filling a sphere ~10-10 meter across. This plum pudding model was generally
accepted. Even Thomson's student Rutherford, who would later prove the
model incorrect, believed in it at the time. But
in 1911 Ernest Rutherford proposed that each atom has a
massive nucleus containing all of its positive charge, and that the much
lighter electrons are outside this nucleus. The nucleus has a
radius about ~ 10-14 - 10-15 m, ten thousand to one hundred thousand times smaller than the radius
of the atom. Rutherford arrived at this model by doing experiments.
He scattered alpha particles off fixed targets and observed some of them
scattering through very large angles. Scattering at large angles
occurs when the alpha particles come close to a nucleus. The
reason that most alpha particles are not scattered at all is that they
are passing through the relatively large 'gaps' between nuclei.
But
in 1911 Ernest Rutherford proposed that each atom has a
massive nucleus containing all of its positive charge, and that the much
lighter electrons are outside this nucleus. The nucleus has a
radius about ~ 10-14 - 10-15 m, ten thousand to one hundred thousand times smaller than the radius
of the atom. Rutherford arrived at this model by doing experiments.
He scattered alpha particles off fixed targets and observed some of them
scattering through very large angles. Scattering at large angles
occurs when the alpha particles come close to a nucleus. The
reason that most alpha particles are not scattered at all is that they
are passing through the relatively large 'gaps' between nuclei.


 Quantum mechanics now predicts what measurements can reveal about atoms.
The hydrogen atom represents the simplest possible atom, since it consists of
only one proton and one electron. The electron is bound, or confined.
Its potential energy function U(r) expresses its electrostatic potential energy
as a function of its distance r from the proton.
Quantum mechanics now predicts what measurements can reveal about atoms.
The hydrogen atom represents the simplest possible atom, since it consists of
only one proton and one electron. The electron is bound, or confined.
Its potential energy function U(r) expresses its electrostatic potential energy
as a function of its distance r from the proton. 




 When an electron changes from one energy level to
another, the energy of the atom must change as well. It requires
energy to promote an electron from a lower energy level to a higher one.
This energy can be supplied by a photon whose energy E is given in terms
of its frequency E = hf or wavelength E = hc/λ.
When an electron changes from one energy level to
another, the energy of the atom must change as well. It requires
energy to promote an electron from a lower energy level to a higher one.
This energy can be supplied by a photon whose energy E is given in terms
of its frequency E = hf or wavelength E = hc/λ. The Balmer lines are designated by H with a Greek subscript in order of decreasing
wavelength. Thus the longest wavelength Balmer transition is designated
H with a subscript alpha, the second longest H with a subscript beta,
and so on.
The Balmer lines are designated by H with a Greek subscript in order of decreasing
wavelength. Thus the longest wavelength Balmer transition is designated
H with a subscript alpha, the second longest H with a subscript beta,
and so on. 
 With these conditions Bohr was able to explain the
stability of atoms, as well
as the emission spectrum of hydrogen. According to Bohr's model only certain
orbits are allowed, which means only certain energies are possible. These
energies naturally lead to the explanation of the hydrogen atom spectrum.
With these conditions Bohr was able to explain the
stability of atoms, as well
as the emission spectrum of hydrogen. According to Bohr's model only certain
orbits are allowed, which means only certain energies are possible. These
energies naturally lead to the explanation of the hydrogen atom spectrum.