Ernest Rutherford discovered that all the positive charge of an
atom was located in a tiny dense object at
the center of the atom. By the 1930s, it was known that this object
was a ball of positively charged protons and electrically neutral neutrons
packed closely together. Protons and neutrons are called
nucleons. The nucleus is a quantum
object. We cannot understand its properties and behaviors using classical
physics. We cannot track the individual protons and neutrons inside a
nucleus. Nevertheless, experiments have shown that the "volume" of
a
nucleus is proportional to the number of nucleons that make up the nucleus.
We define the volume of the nucleus (and also the volume of any other quantum
particle) as the volume of the region over which its interaction with the
outside world differs from that of a point particle, i.e. a particle with no
size.
With the above definition of the volume and size of a quantum
particle we find that protons and neutrons are each about 1.4*10-15 m
in diameter, and the size of a nucleus is essentially the size of a ball of
these particles. For example, iron 56, with its 26 protons and 30
neutrons, has a diameter of about 4 proton diameters. Uranium 235 is just
over 6 proton diameters across. One can check, for example, that a bag
containing 235 similar marbles is about six marble diameters across.
Most nuclei are approximately spherical. The average radius of a
nucleus with A nucleons is R = R0A1/3, where R0
= 1.2*10-15 m. The volume of the nucleus is directly
proportional to the total number of nucleons. This suggests that all
nuclei have nearly the same density. Nucleons combine to form a nucleus as
though they were tightly packed spheres.
Link: Dense packing of spheres
What is the density of nuclear matter?
Solution:
Find the radius of a 238Pu nucleus. 238Pu is a manufactured nuclide that is used as a power source on some space probes. I contains 238 nucleons.
Solution:
Find the diameter of a 56Fe nucleus.
Solution:
That the nucleus exists means that there is some force other than the electrostatic force or gravity which holds it together. The protons are all repelling each other electrically, the neutrons are electrically neutral, and the attractive gravitational force between protons is some 10-38 times weaker than the electrostatic repulsive force. The force that holds the nucleus together must be attractive and even stronger than the electrostatic repulsion. This attractive force is called the nuclear force. The nuclear force treats protons and neutrons equally, it does not differentiate between a proton and a neutron. The nuclear force is charge independent. For this reason we talk about the nuclear force between nucleons. The nuclear force does not act on electrons. The properties of the nuclear force can be deduced from the properties of the structures it creates, namely the atomic nuclei. The fact that protons and neutrons maintain their size while inside a nucleus means that the nuclear force is both attractive and repulsive. If we try to pull two nucleons apart, the attractive nuclear force holds them together, next to each other. But if we try to squeeze two nucleons into each other, we encounter a very strong repulsion, giving the nucleons essentially a solid core. It is the repulsive part of the nuclear force that makes nuclear matter nearly incompressible.
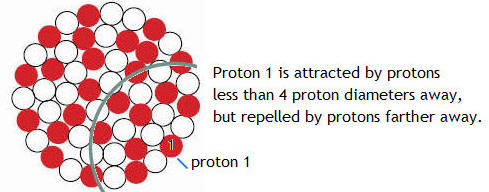
While the attractive nuclear force must be stronger than the electrostatic force to hold the protons together in the nucleus, it is not a long range 1/r2 force like the electrostatic force and gravity. It drops off much more rapidly than 1/r2, with the result that if two protons are separated by more than a few proton diameters, the electric repulsion becomes stronger than the nuclear attraction. The separation D0 at which the electric repulsion becomes stronger than the nuclear attraction is about 4 proton diameters. This distance D0, which we will call the range of the nuclear force, can be determined by looking at the stability of atomic nuclei. If we start with a small nucleus, and keep adding nucleons, for a while the nucleus becomes more stable if we add the right mix of protons and neutrons. By more stable, we mean more tightly bound. The more stable a nucleus is, the more energy is required, per nucleon, to pull the nucleus apart. This stability is caused by the attractive nuclear force between nucleons.
Iron 56 is the most stable nucleus. It is most efficiently bound and has the lowest average mass per nucleon. Nickel 62, Iron 58 and Iron 56 are the most tightly bound nuclei. It takes more energy per nucleon to take one of these nuclei completely apart than it takes for any other nucleus. If a nucleus gets bigger than these nuclei, it becomes less stable. If a nucleus gets too big, bigger than a Lead 208 or Bismuth 209 nucleus, it becomes unstable and decays by itself. The stability of Iron 56 results from the fact that an Iron 56 nucleus has a diameter about equal to the range of the nuclear force. In an Iron 56 nucleus every nucleon is attracting every other nucleon. If we go to a nucleus larger than Iron 56, then neighboring nucleons still attract each other, but protons on opposite sides of the nucleus now only repel each other. This repulsion between distant protons leads to less binding energy per particle and instability. We usually give the binding energy of a nucleus as a positive number. It then is the energy that is needed from an external source to separate the nucleus into its constituent protons and neutrons.
The simplest nucleus is a single proton. It is the nucleus of hydrogen. The proton is an elementary particle of mass m = 1.67*10-27 kg and mass energy of about E = mc2 = 940 MeV. (Note: Often the mass of a quantum particle is given in units of mass energy, E = mc2. So you will often read that the mass of the proton is ~940 MeV.) The proton has one unit of positive charge and spin ½. It is a or fermion and obeys the Pauli exclusion principle. No two protons can be in exactly the same quantum state. The next simplest nucleus is the deuteron. It is a bound state of a proton and a neutron. The neutron, like the proton, is a spin ½ fermion, but it has no electric charge, and is slightly more massive than the proton. The binding energy of the deuteron, or the energy it takes to tear apart a deuteron into a free proton and a free neutron, is 2.2 MeV. A photon of this energy could "ionize" the deuteron into a separated proton and neutron. However, it is not necessary to actually do this experiment to establish how tightly the deuteron is bound. One only needs to weigh the deuteron accurately. It has a mass of 1875.61 MeV. The proton has a mass of 938.27 MeV, the neutron 939.56 MeV, so the sum of their masses is 1877.83 MeV, 2.2 MeV more than the deuteron mass. Thus, when a proton and a neutron come together to form a deuteron, they must release 2.2 MeV of energy, which they do by emitting a γ ray. The total number of nucleons in a nucleus is usually denoted by the mass number A, where A = Z + N, Z protons and N neutrons. The chemical properties of an atom are determined by the number of electrons, the same as the number of protons Z. This is called the atomic number. Nuclei can have the same atomic number, but different numbers of neutrons. These nuclei are called isotopes, the Greek for "same place", since they are in the same place in the periodic table.
We use the following notation to describe a nucleus:AZX, where X is the chemical symbol of the element.
2713Al
Discuss this with your fellow students in the discussion forum!
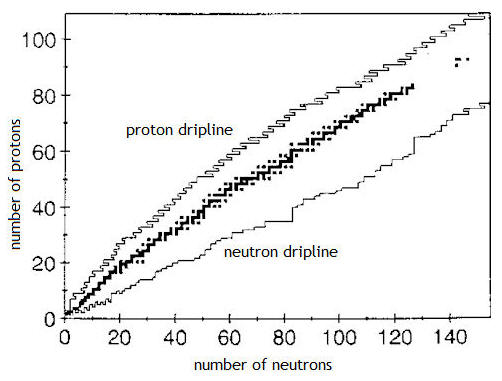Physicists map the inventory
of known nuclei on a "chart of nuclides." On the chart shown on
the right, the vertical axis represents the number of protons a nucleus
contains and the horizontal axis represents the number of neutrons it
possesses. The region of stable nuclei is roughly found on a
diagonal line, where the neutron number approximately equals proton
number. Below this diagonal is a jagged line called the "neutron
dripline" and above this diagonal is another jagged line called the
"proton dripline." Nuclei found above the proton dripline and
below the neutron dripline tend to be highly unstable and undergo
radioactive decay immediately.
Link: Interactive
Chart of Nuclides
(The horizontal axis of this chart represents the number of neutrons and
the vertical axis represents the number of protons.)
The best way to see the competition between the
attractive nuclear force and the electric repulsive force inside atomic
nuclei is to look at nuclear binding energies.
The binding energy represents how much
energy we would have to supply to pull the nucleus apart into separate
free nucleons. The nuclear force tries to hold the nucleus
together and therefore increases the binding energy. The
electrostatic force, which pushes the protons apart, decreases the
binding energy. We calculate the binding energy of a nucleus by
subtracting the rest energy of the nucleus from the sum of the rest
energies of the protons and neutrons that make up the nucleus. We
then divide by the number of nucleons to get the
binding energy per nucleon. For the deuteron the
binding energy per nucleon is therefore 1.1 MeV.
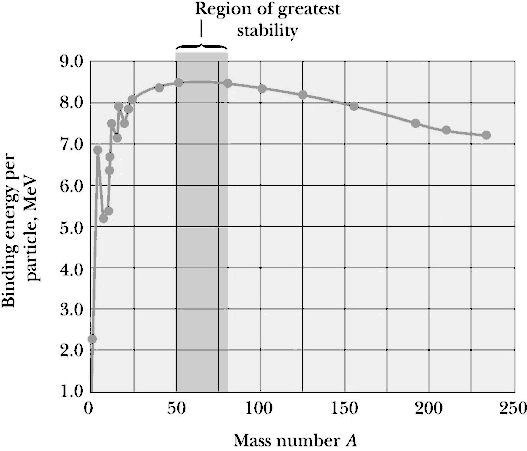
The figure on the
right is a plot of the binding energy, per nucleon, of the most stable
nucleus for each element. The peak of that curve is at the Iron 56
nucleus, no other nucleus is more tightly bound. Except for light
nuclei, the binding energy is about 8 MeV per nucleon.
Moving towards higher binding energy represents a release of energy.
There are two ways to do this. We can start with light nuclei and put
them together to form heavier nuclei, moving in and up from the left
side in the figure. This process is called nuclear fusion. Or we
can split apart heavy nuclei moving in and up from the right side.
This process is called nuclear fission. Fusion represents the
release of nuclear potential energy, while fission represents the
release of electric potential energy. When we get to Iron 56, there is
no energy to be released either by fusion or fission.
The importance of knowing the nuclear binding energy per nucleon is that it tells us whether energy will be released in a particular nuclear reaction. If the somewhat weakly bound uranium nucleus (7.41 MeV/ nucleon) splits into two more tightly bound nuclei like cesium (8.16 MeV/nucleon) and zirconium (8.41 MeV/ nucleon), energy is released. At the other end of the graph, if we combine two weakly bound deuterium nuclei (2.8 MeV/nucleon) to form a more tightly bound Helium 4 nucleus (7.1 MeV/nucleon), energy is also released. Any reaction that moves us toward the Iron 56 nucleus releases energy.
Given the mass of the alpha particle, mc2 = 3727.38 MeV, find the binding energy per nucleon.
Solution:
Atomic and nuclear data tables often list the mass of the neutral atom (not that of the nucleus) in atomic mass units (u). Atomic masses include the masses of the atomic electrons, and thus are not equal to the nuclear masses. One u is (1/12)th of the mass of the neutral carbon atom , 1 u = (1/12)m12C. This can easily be converted to SI units. One mole of 12C has a mass of 0.012 kg, and contains Avogadro's number particles, thus
1 u = (0.001 kg)/NA = 1.66054*10-27 kg = 931.494 MeV/c2.
We can write down a formula for the binding energy of a nucleus in terms of
the nuclear masses or in terms of the atomic masses. The binding energy is
defined as the the total mass energy of constituent nucleons minus the mass
energy of the nucleus. It is the total energy one needs to invest to
decompose the nucleus into nucleons.
In terms of the nuclear masses, we write for the
binding energy B(Z,N) of a nucleus with Z protons and N neutrons
B(Z,N) = c2(Z*mp + N*mn - Mnuc(Z,N)).
In terms of the atomic masses, we write
B(Z,N) = c2(Z*mH + N*mn - Matom(Z,N)).
The masses of the Z electrons cancel out and the difference in binding energies of the electrons in the different atoms (~eV) is negligible compared to the nuclear binding energy (~MeV).
Binding energy of the alpha particle terms of of atomic mass units
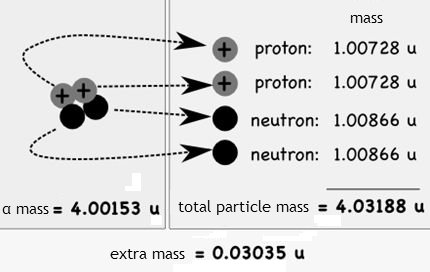
Binding energy: 28.3 MeV
What is the binding energy per nucleon for 120Sn?
Solution:
What is the binding energy per nucleon for 262Bh? The mass of the atom is 262.1231 u.
Solution: