The magnetic force on a moving charge
Moving electric charges produce magnetic fields.
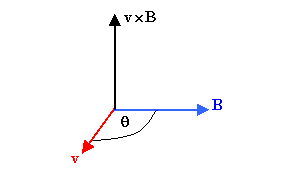Magnetic fields exert forces on other moving charges.
The force a magnetic field exerts on a charge q moving with velocity
v is called the magnetic
Lorentz force.
It is given by
F = qv × B.
(The
SI unit of B is Ns/(Cm) = T (Tesla))
The force F is perpendicular to the direction of the magnetic
field B.
It also is perpendicular to the direction of the velocity v.
F is perpendicular to the plane that contains both v and
B.
(Review the
vector or cross product!)
The magnitude of the Lorentz force F is F = qvB sinθ, where θ is
the smallest angle between the directions of the vectors v and
B.
If v and B are parallel or anti-parallel to each other,
then sinθ = 0 and F = 0. If v and
B are
perpendicular to each other, then sinθ = 1 and F has its maximum
possible magnitude F = qvB.
If a charge q is moving with uniform velocity
v parallel to
the direction of a uniform magnetic field B, it experiences no
force. It continues to move with uniform velocity v along a
straight line parallel to the field.
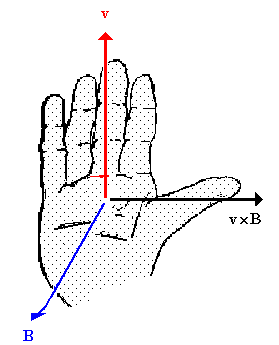To find the direction of the
Lorentz force, use the
right-hand rule (Vector Product). Let the fingers of your
right hand point in the direction of v. Orient the palm of
your hand, so that as you curl your fingers, you can sweep them over to
point into the direction of B. Your thumb points in the
direction of the vector product v × B. If q is
positive then this is the direction of F. If q is negative,
your thumb points opposite to the direction of F.
Problem:
On the surface of a pulsar, or neutron star, the magnetic field may be as
strong as 108 T. Consider the electron in a hydrogen atom on
the surface of the neutron star. The average distance between the electron
and the proton is 0.53*10-10 m. The average speed of the
electron is 2.2*106 m/s. Compare the magnitude of the electric force that the
electric field of the proton
exerts on the electron with the maximum magnitude of the magnetic force that the magnetic field of the
neutron star exerts on the electron. Is it reasonable to expect that the
hydrogen atom will be strongly deformed by the magnetic field?
Solution:
- Reasoning:
The electron in a hydrogen atom is at a distance r = 0.53*10-10
m from the proton.
The magnitude of the electric force acting on the electron is
equal to Fel = keqe2/r2.
The maximum magnitude of the magnetic force acting on the electron when its velocity
v is perpendicular to B is Fmag = qevB.
- Details of the calculation:
Fel = keqe2/r2
= 9*109*(1.6*10-19)2/(0.53*10-10)2
N = 8.2*10-8 N.
Fmag = qevB = 1.6*10-19*2.2*106*108
N = 3.5*10-5 N.
The maximum magnitude of the magnetic force on the electron is more than 1000 times stronger than
the magnitude of the electric force. We expect that hydrogen atoms will be strongly deformed
or destroyed on the surface of a neutron star.
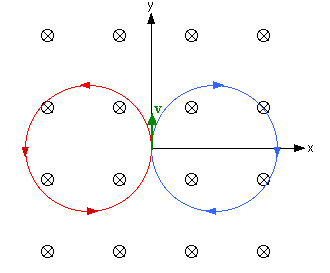Consider a charged particle with mass m and charge q
which at t = 0 has a velocity v perpendicular to
B.
This particle experiences a force with magnitude F = qvB perpendicular
to its velocity. A force perpendicular to the velocity results in
centripetal acceleration
a = F/m = v2/r. The
particle will move along a circular path. The radius of the circle
is
r = mv2/F = mv2/(qvB) =
mv/(qB),
and the circle lies in a plane perpendicular to
B. The
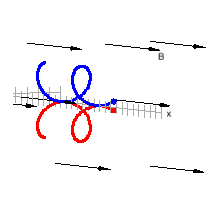
diagram on the right shows the paths followed by two charges, one
positive (red) and one negative (blue), in a magnetic field that points
into the page.
Since the magnetic force is perpendicular to the
velocity v = ∆r/∆t, it is, at any time, perpendicular to
the displacement ∆r. The work done by the magnetic force is
therefore zero, ∆W = F∙∆r = 0.
The magnetic force does no work.
The magnetic force changes
the direction of the velocity, but it does not change the speed or the
kinetic energy of the particle.
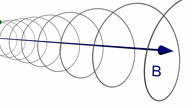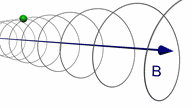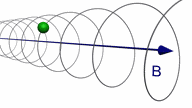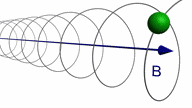Assume a particle at t = 0 is moving
with a velocity v which has a component vperpendicular
perpendicular and a component vparallel parallel to
the magnetic field.
The path of the particle will be a spiral.
There is no acceleration parallel to B, but in the
plane perpendicular to B the centripetal acceleration
is a = qvperpendicularB/m, and the particle moves in a circle.
The superposition of these two motions results in a spiral path.
An interactive 3D animation of the motion of a charged particle in a uniform magnetic field.
Click here!
The magnetic force on a current-carrying wire
In a current carrying wire electrons move with an average velocity, called
the drift velocity vd. If the wire is placed into a
magnetic field B, a force will act on the wire.
Consider a straight section of wire of length L. The number of
moving electrons in this section is n-AL, where n-
is the electron density and A is the cross-sectional area of the wire. The
electrons move with the drift velocity vd. The force
F
on the section of wire is the sum of the forces on all the moving electrons,
F = -qn-ALvd × B
= jAL × B = IL × B.
Here we have used that -qn-vd = ρ-vd
= j, and that jA = I for a wire. Since I is not a vector and
we have to preserve the directional aspects of the vector product, we assign the
direction of the current density to L, which points in the
direction as j.
The force on a straight section of wire in a uniform field
B
is
F =
IL × B.
You can again use the right-hand rule to find the direction of the force.
Let the fingers of your right hand point in the direction of the current flow.
Orient the palm of your hand, so that as you curl your fingers, you can sweep
them over to point into the direction of B. Your thumb points in
the direction of the vector product F.
Problem:
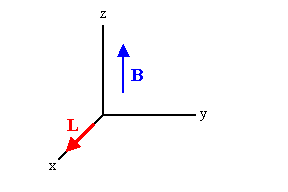A wire carries a steady current of 2.4 A. A
straight section of the wire is 0.75 m long and lies along the x-axis
within a uniform field B = 1.6 T in the z-direction. If the
current is in the positive x-direction, what is the magnetic force on
the section of wire.
Solution:
- Reasoning:
The force on the wire is given by F
= IL × B.
The direction of
L × B is the negative y-direction. Since L and B are perpendicular to each other, the magnitude F = ILB.
- Details of the calculation:
F = ILB
= (2.4 A)(0.75 m)(1.6 T) = 2.88 N.
The force on the section of wire is
F = -2.88 N j, in the
negative y-direction.
External link:
The Lorentz force
on a wire (Youtube)
Embedded Question 1
A demo: We pass a current through a wire a section of which passes
between the poles of two magnets, as shown below.
Make a prediction. When we connect the power supply, which way the wire will
move?
Discuss this with your fellow students in the discussion forum!
Review with them the Lorentz force and the right-hand rule.
In this
video clip a hand crank generator is used to produce a voltage across
a thin rod which can move in a magnetic field produced by a set of magnets.
The north pole of the magnets points up.
When
the crank is turned in the direction of the arrow shown, the red lead is
positive, and a current flows from the left to the right through the rod.
If the crank is turned the other way, a a current flows from the right to the
left through the rod.
You can verify that the direction of the force F on the wire is the
direction of IL × B.
Problem:
Two parallel wires both carry current flowing in the same direction. Do
the wires attract or repel each other?
Solution:
- Reasoning:
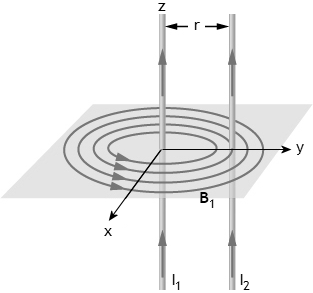
Choose the coordinate system so that the currents flow in the z direction.
Let the second wire cross the y-axis at y = r.
The magnetic field B1 due to I1 in wire 1
encircles wire 1. it points in the negative x-direction at the
position of wire 2
The force on wire 2 is given by F12 = I2L2
× B1.
The direction of
L2 × B1 is the negative y-direction.
The force wire 1 exerts on wire 2 points in the negative y-direction,
towards wire 1.
Wire 1 attracts wire 2, By Newton's third law, wire 2 attracts wire 1.
Remember: Parallel wires carrying currents in the same direction
attract each other, parallel wires carrying currents in opposite directions
repel each other.
External link:
Two wires (Youtube)
If you miss having regular lectures, consider this video lecture.
Lecture 11:
Magnetic field and Lorentz Force