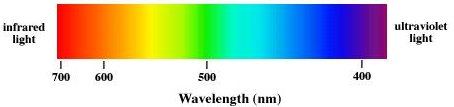
Electromagnetic waves are categorized according to their frequency f or, equivalently, according to their wavelength λ = c/f. Visible light has a wavelength range from ~400 nm to ~700 nm. Violet light has a wavelength of ~400 nm, and a frequency of ~7.5*1014 Hz. Red light has a wavelength of ~700 nm, and a frequency of ~4.3*1014 Hz.
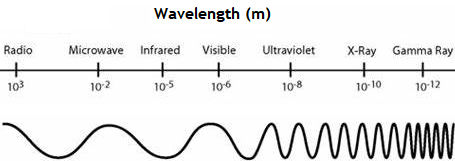
Visible light makes up just a small part of the full electromagnetic spectrum. Electromagnetic waves with shorter wavelengths and higher frequencies include ultraviolet light, X-rays, and gamma rays. Electromagnetic waves with longer wavelengths and lower frequencies include infrared light, microwaves, and radio and television waves.
| Type of Radiation | Frequency Range (Hz) | Wavelength Range |
|---|---|---|
| gamma-rays | 1020 - 1024 | < 10-12 m |
| x-rays | 1017 - 1020 | 1 nm - 1 pm |
| ultraviolet | 1015 - 1017 | 400 nm - 1 nm |
| visible | 4 - 7.5*1014 | 750 nm - 400 nm |
| near-infrared | 1*1014 - 4*1014 | 2.5 μm - 750 nm |
| infrared | 1013 - 1014 | 25 μm - 2.5 μm |
| microwaves | 3*1011 - 1013 | 1 mm - 25 μm |
| radio waves | < 3*1011 | > 1 mm |
Two microwave frequencies are authorized for use in microwave ovens, 900 and 2560 MHz. Calculate the wavelength of each.
Solution:
Distances in space are often quoted in units of light
years, the distance light travels in one year.
(a) How many meters is a light year?
(b) How many meters is it to Andromeda, the nearest large galaxy, given
that it is 2.54*106 light years away?
(c) The most distant galaxy yet discovered is 12*109 light
years away. How far is this in meters?
Solution:
What can we learn by analyzing the EM spectrum emitted by a source?
The velocities of particles with thermal energy are changing almost all the time. The particles are accelerating. Accelerating charged particles produce electromagnetic radiation. The power radiated is proportional to the square of the acceleration. Higher rates of velocity change result in higher frequency (shorter wavelength) radiation. The observed intensity of thermal radiation emitted by as a function of wavelength can be described by the Planck Radiation Law (Physics 221).
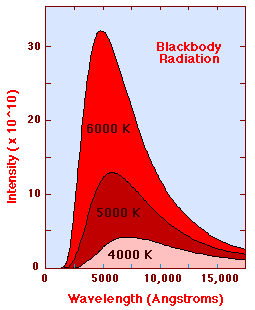The Planck Radiation Law gives the
intensity of radiation as a function of wavelength for a fixed temperature.
The Planck law gives a continuous distribution, which peaks at some wavelength.
The peak shifts to shorter wavelengths for higher temperatures, and the area
under the curve grows rapidly with increasing temperature. The diagram
below shows the intensity distribution predicted by the Plank law in J/(m2s)
for blackbodies at various temperature. By observing the continuous
distribution of the thermal radiation emitted by an object, we can learn its
temperature.
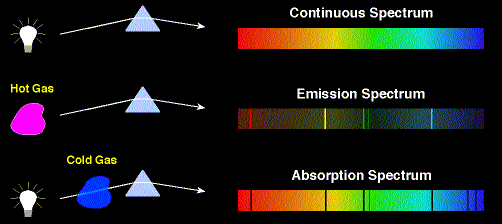
When light passes through or reflects or scatters of matter, it interacts with the atoms and molecules. Atoms and molecules have characteristic resonance frequencies. The preferentially interact with light waves of exactly those frequencies. When excited in collisions, atoms and molecules emit light with a set of characteristic frequencies. This results in a line spectrum. Only light with a discrete set of wavelengths is produced and the spectrum is not continuous, but consist of a set of emission lines. That set characterizes the atoms and molecules which produced it and can be used to identify those atoms and molecules and their environment.
When light with a continuous
distribution of wavelengths passes through a low-density material, the atoms and
molecules of the material absorb light waves with the same set of characteristic
frequencies that appear in their emission spectrum. This produces an absorption
spectrum, a nearly continuous spectrum with missing lines. The absorption
spectrum can also be used to identify those atoms and molecules and their
environment.
Please explore this simple simulations of various molecules interacting with
electromagnetic radiation of different wavelength.
https://phet.colorado.edu/en/simulations/molecules-and-light
Can you identify certain characteristics?
Discuss this with your fellow students in the discussion forum!