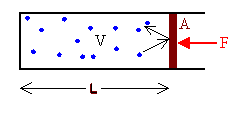
 Assume we have a collection of gas molecules in gravity-free space in a container with volume V at
absolute temperature T.
Assume we have a collection of gas molecules in gravity-free space in a container with volume V at
absolute temperature T.  Assume we have a collection of gas molecules in gravity-free space in a container with volume V at
absolute temperature T.
Assume we have a collection of gas molecules in gravity-free space in a container with volume V at
absolute temperature T.
Then each molecule moves along with constant velocity in a straight line, until it hits another molecule, or a container wall. A collision between two molecules is similar to a collision between two balls. The molecules exchange momentum, but the total momentum of the two molecules is conserved. When a molecule hits a wall, it bounces back. Its momentum changes. To change the molecule's momentum, the wall must exert a force on the molecule. Newton's third law tells us that the molecule exerts a force on the wall. The greater the number of molecules hitting a wall, the greater is the force on the wall. In a container with different size walls, the bigger walls will receive more hits than the smaller walls and therefore experience a greater force. The pressure in the container is the magnitude of the normal force F on a wall divided by the surface area A of the wall.
P = F/A
 The faster the molecules move in the container, the greater is the change in
momentum when they bounce off a wall, and the more often do they hit the walls.
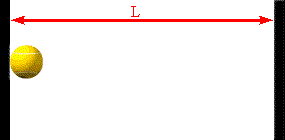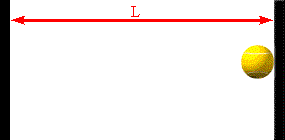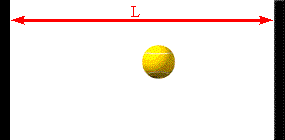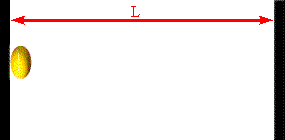
Assume a molecule moves horizontally with speed |vx| back and forth
between two infinitely-massive walls, which are a distance L apart. When
it hits the right wall its momentum changes from p1 = +m|vx|
to p2 = -m|vx|. The change in the molecule's
momentum is Δpmol = p2
- p1 = -2m|vx|. The time interval between successive
hits on the right wall is Δt = 2L/|vx|. So the average force
the wall exerts on this molecule is Fmol
= Δpmol/Δt = -2m|vx|/(2L/|vx|) = -mvx2/L.
By Newton's third law, the average force that the molecule exerts on the wall is
Fwall
= mvx2/L, it is proportional to the square of the
speed of the molecule or its kinetic energy.
The faster the molecules move in the container, the greater is the change in
momentum when they bounce off a wall, and the more often do they hit the walls.
Assume a molecule moves horizontally with speed |vx| back and forth
between two infinitely-massive walls, which are a distance L apart. When
it hits the right wall its momentum changes from p1 = +m|vx|
to p2 = -m|vx|. The change in the molecule's
momentum is Δpmol = p2
- p1 = -2m|vx|. The time interval between successive
hits on the right wall is Δt = 2L/|vx|. So the average force
the wall exerts on this molecule is Fmol
= Δpmol/Δt = -2m|vx|/(2L/|vx|) = -mvx2/L.
By Newton's third law, the average force that the molecule exerts on the wall is
Fwall
= mvx2/L, it is proportional to the square of the
speed of the molecule or its kinetic energy.
Assume that there are N molecules in the volume V, moving horizontally with
speed |vx|. Not all the molecules have the same
kinetic energy. The force
exerted by the molecules on the walls of a container is therefore F = Nm<vx2>/L,
where <vx2> is the average value of vx2.
The pressure is P = F/A = Nm<vx2>/V,
since L*A = V. With ρparticle = N/V we have
P = F/A = ρparticlemvx2.
There is nothing special about the x-direction. The atoms can move up and down, back and forth, in and out. The average velocity components in all directions are all going to be equal to each other.
<vx2> = <vy2> = <vz2>.
They are each equal to one-third of their sum, which is the square of the magnitude of the average velocity.
<v2> = <vx2> + <vy2>
+ <vz2>.
<vx2> = (1/3)<v2>.
We may therefore write
P = (1/3)ρparticlem<v2> = (2/3)ρparticle(m<v2>/2).
This equation relates the pressure to the kinetic energy of the atoms or molecules, since m<v2>/2 is the kinetic energy of the center-of-mass or translational motion of an atom or molecule. Using ½m<v2> = (3/2)kBT and ρparticle = N/V from above we therefore find that
PV = (2/3)N(m<v2>/2).
PV = NkBT.
The pressure in a container is proportional to the average kinetic energy of the molecules and therefore to the absolute temperature T of the gas.
If all the molecules in a container would be at rest, their kinetic energy would be zero and the pressure would be zero.