Refraction and reflection
In this lab you will explore the behavior of light at the boundary
between two transparent media with different indices of refraction. A
fraction of the incident intensity will be reflected, and the rest of the light
will be transmitted. The direction of propagation of the reflected and
transmitted light is given by the laws of reflection and refraction.
-
Law of reflection: θi = θr
- Snell's law or law of refraction:
nisinθi = ntsinθt.
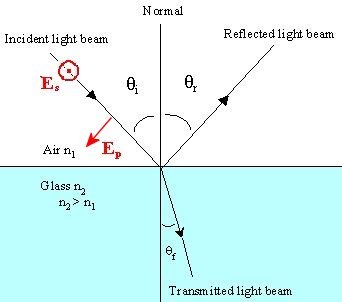 How much of the light is reflected and how much is transmitted?
How much of the light is reflected and how much is transmitted?
The reflectance R is the ratio of the reflected
flux to the incident flux, and the transmittance
T is the ratio of the transmitted flux to the incident flux.
Energy conservation requires that R + T = 1 (if there is no absorption).
R and T depend on the indices of refraction of the two media n1
and n2, the angle of incidence θi,
and the polarization of the incident light.
We distinguish between
p-polarization and s-polarization.
Consider, for example, an air-glass interface as shown. The plane of incidence contains the normal to the boundary and the
incident ray. The electric field vector E of the incident
wave is perpendicular to the direction of propagation and can have a component in the plane of incidence,
Ep,
and a component perpendicular to the plane of incidence Es.
We have E = Ep+
Es.
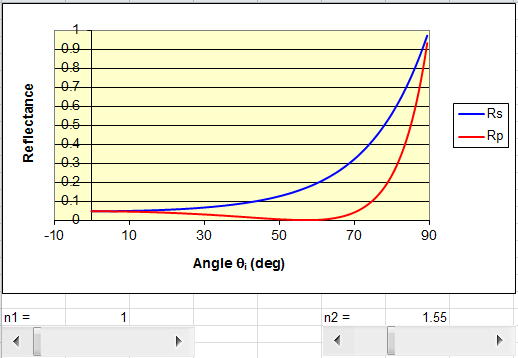 The reflectance R depends of the polarization and is given for p-polarization by
The reflectance R depends of the polarization and is given for p-polarization by
Rp = ((tan(θi - θt)/tan(θi
+ θt))2,
and for s-polarization by
Rs = ((sin(θi - θt)/sin(θi
+ θt))2.
If θ1 + θ2 = π/2, then tan(θ1
+ θ2) = infinite and Rp = 0. If light is reflected, it
will have s-polarization. The incident angle at which this happens
is called the Brewster angle θB. We then have
n1sinθB = n2sin((π/2) -θB) = n2cosθB.
tanθB = n2/n1.
Explore using this spreadsheet.
Vary n1 and n2 and observe the changes.
Reflection and refraction can result in
image formation. Spherical
mirrors form images by reflection. The mirror equation tells us
where the image is formed and if it is real or virtual.
- mirror equation: 1/xo
+ 1/xi = 1/f
- magnification: M = hi/ho=
-xi/xo
If the magnification is negative, the
image is inverted.
Things that always go together for spherical mirrors:
- real image <--> inverted image <--> xi is positive
<--> M is negative
- virtual image <--> upright image <--> xi is negative
<--> M is positive
xo and xi are positive for locations in front
of the mirror and negative for locations behind the mirror. R and f are positive for concave and negative for convex mirrors,
and f = R/2.
In this session you will explore refraction at a plane
interface and image formation by reflection from spherical surfaces.
Open a Microsoft Word document to keep a log of your procedures,
results and discussions. This log will become your lab report. Address the
points highlighted in blue. Answer all questions.
Refraction
Exploration 1
Use an on-line simulation from the University of Colorado PhET group to explore
the bending of light.
Link to the simulation:
https://phet.colorado.edu/en/simulations/bending-light
Explore the interface!
-
Tools and objects can be dragged out of the tool box and then returned.
-
The objects in the Prisms tab can be rotated by dragging the handle.
-
In the Prisms tab, the protractor rotates and the laser translates.
-
All the tools work in both Ray and Wave mode, but some are easier to use in
Wave mode because the region where the tool can read is larger.
Click on either the Intro or More Tools tab. Let red light move from air
into water. (Make sure you select water if you click the More Tools tab.)
For incident angles θi from zero to 80o in 10 degree steps
measure the angle of refraction θt and the reflected intensity or
reflectance R.
Download this spreadsheet and
enter your measured values on sheet 1.
- Plot R versus theta. Paste your graph into your log. Compare to
the graph above.
- Discuss your result.
- Is the laser light p-polarized, s-polarized, or unpolarized. What do
your results suggest?
- Calculate sinθi and sinθt. Remember that Excel
functions require the angles to be in radians.
The first row if the spreadsheet already contains the formulas.
- Plot sinθi versus sinθt.
- What does the plot look like?
- Use the trendline to find the slope. Paste the graph with trendline
into your log.
- What value do you obtain for the slope?
- Given Snell's law, what value do you expect for the slope? Discuss!
(b) Design experiments to determine the index of refraction of mystery
materials A and B.
- Describe your procedure and discuss why you decided to
proceed this way. What are your results for nA
and nB?
(c) Design and describe a setup that has the refracted ray bend away
from the normal?
- Paste a screen shot of your setup into your log.
(d) Click on the prism break tab. Use red light with a wavelength
of 650 nm. Try to arrange various prisms in such a way, so that the laser
beam after total internal reflections moves parallel to the incident beam but in
the opposite direction. Try to use as few pieces as possible.
- Paste a screen shot of your design into your log.
(e) Now switch to white light and experiment with various prisms to
answer the following questions.
- Are the reflection and refraction of light color-dependent? How can
you tell?
- Which shapes split the white light into different colors the best? Did
you find a set-up that demonstrates this well?
- Try to arrange a situation so that the light light forms a rainbow.
What shape did you choose?
Reflection
Exploration 2:
Explore image formation with spherical mirrors. Use this
interactive
simulation.
- You can choose the radius of curvature of the mirror R (positive or
negative), the object position xo = o, and the height of the object ho = h.
- The simulation calculates the image position xi and the
height of the image hi.
- The simulation also draws a ray diagram.
Investigate 4 different situations and fill out the
table on sheet 3 of your spreadsheet. You choose the radius of curvature R
and the object position xo.
- Use a concave mirror to produce a real image which is bigger that
the object.
- Use a concave mirror to produce a real image which is smaller that
the object.
- Use a concave mirror to produce a virtual.
- Use a convex mirror to produce an image.
| case |
R |
f |
xo |
xi |
1/x0 + 1/xi |
1/f |
M |
image
real? |
image
upright? |
concave mirror, real image:
|hi| > |ho| |
|
|
|
|
|
|
|
|
|
concave mirror, real image:
|hi| < |ho| |
|
|
|
|
|
|
|
|
|
concave mirror, virtual image
|
|
|
|
|
|
|
|
|
|
convex mirror
|
|
|
|
|
|
|
|
|
|
- Paste the table into your log.
- Discuss your results.
- Can you think of situations where spherical
mirrors are used to produce the images explored in case 1 - 4.
Experiment
In this experiment you will trace the path of a light ray through a block of
glass and measure the index of refraction of the glass. For an air-glass
boundary we can set the index of refraction of air equal to one. Snell's
law therefore yields for the index of refraction of the glass
nglass = sinθair/sinθglass.
It is easy to measure θair, but not θglass inside the
glass. But when a light ray enters square block of glass from air making a
nonzero angle θair with the normal to the interface, the ray is bent
towards the normal as its enters and away from the normal as it leaves the glass
block. The emergent ray moves in the same direction as the incident ray,
but is displaced parallel to the incident ray. The parallel displacement d
depends on index of refraction nglass and the width w of the block.
By measuring the displacement d, we can determine nglass.
Procedure:
Click to open the
"optics lab"
simulation.

It contains a laser, an optical breadboard and several optical components.
The components can be dragged to different positions on the breadboard and the
components can snap to the holes on the breadboard which have a spacing of 1
unit = 2.5 cm. The screen is 4 units wide and 2 units high and the lines
on the screen are spaced by ½ unit. Clicking anywhere on the breadboard
you can rotate and zoom the view.
When the simulation opens the laser beam passes through a glass block.
The dimensions of the glass block are 2.8 by 2.8 by 1.4 units.
- Drag the glass block out of the way and position the screen so that the
undeflected beam hits the middle of the screen.
- Keep the rotation angle of the glass block at 0o and drag the
glass block back into position so that the laser beam passes through the
block and hits the middle of the screen.
- Click the "Rotate postholder" button and rotate the glass block until
the laser beam is displaced by d = 1/4 unit. Remember that the lines
on the screen are spaced by ½ unit. Decrease the beam radius to its
minimum value so that you can make a more precise measurement. You can
also drag the screen close to the glass block, and you can rotate an zoom
the view.
- Record the angle θair corresponding to d = 1/4 unit in your
spreadsheet on sheet 2.
- Repeat for d = ½ unit, 3/4 unit and 1 unit, for a total of 4
measurements.
Data Analysis:
Use your measurements to determine the index of refraction nglass
of the glass block.
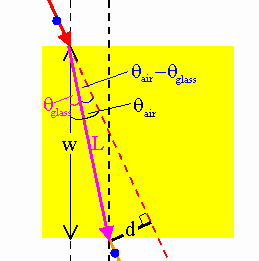 The expected
displacement of a ray passing through the glass block is d. From the
figure on the right we see that
The expected
displacement of a ray passing through the glass block is d. From the
figure on the right we see that
d/L = sin(θair - θglass),
w/L = cos(θglass).
This can be rewritten as
d = wsin(θair - θglass)/cos(θglass),
and applying Snell's law and trigonometric relations
d = w sinθair[1 - cosθair/(nglass2
- sin2θair)½].
This equation can be solved for nglass.
nglass2 = cos2θair/(1
- d/(w sinθair))2 + sin2θair.
Use your spreadsheet to calculate nglass for
each of your 4 measurements. Paste your spreadsheet table into your log.
- Do your measurements agree with each other within
reasonable uncertainty, given how you performed your measurements.
- Do you suspect some of the measurements to be more accurate than others?
If yes, why?
- From your measurements, what do you conclude is the index of refraction n ±
Δn of the glass block?
Convert your log into a lab report.
See the grading scheme for all lab
reports.
Name:
E-mail address:
Laboratory 7 Report
- In one or two sentences, state the goal of this lab.
- Make sure you completed the entire lab and answered all parts. Make
sure you show your work and inserted and properly labeled relevant tables
and plots.
- Add a reflection at the end of your report in a short essay format.
Save your Word document (your name_lab7.docx), go to Canvas, Assignments, Lab
7, and submit your document.
 How much of the light is reflected and how much is transmitted?
How much of the light is reflected and how much is transmitted? The reflectance R depends of the polarization and is given for p-polarization by
The reflectance R depends of the polarization and is given for p-polarization by

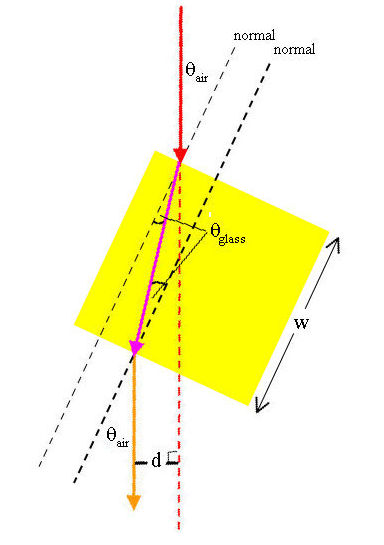

 The expected
displacement of a ray passing through the glass block is d. From the
figure on the right we see that
The expected
displacement of a ray passing through the glass block is d. From the
figure on the right we see that